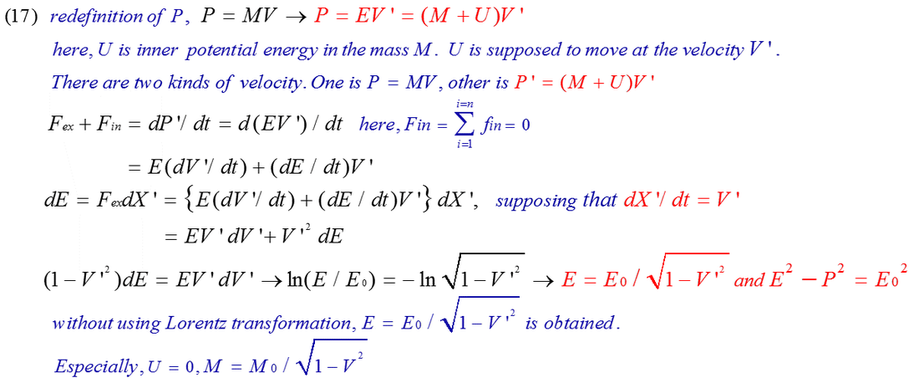What is rest mass ? by Nobuo Miyaji e-mail nobuo.miyaji@hotmail.co.jp
dated June 20th, 2012
the latest rev. March 28th, 2020
Preface
Many people get confused about the concept of rest mass in the theory of Special Relativity.
Scientists have deliberated over a rest mass (Gary Oas1, L.B.Okun2 , Max Jammer3).
A single rest mass has been thought to be equivalent to rest energy because relativistic mass is divided into rest mass
and kinetic energy according to Taylor expansion. However, there remains a question on what rest mass is. This article aims
to indicate the concept of rest mass. The common definition that rest mass is the observed mass with no kinetic energy is not
complete. A group of moving masses with arbitrary velocity also forms an equivalent rest mass.
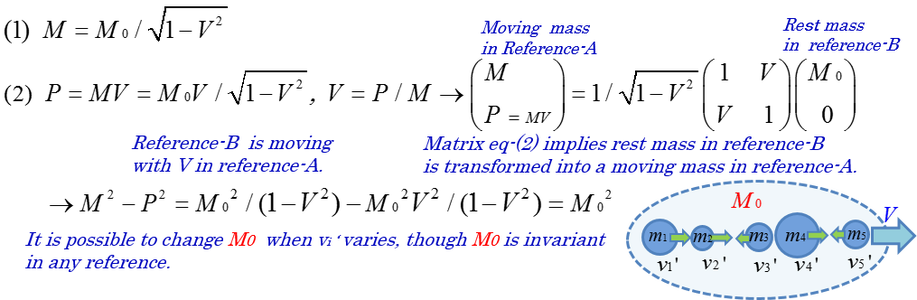
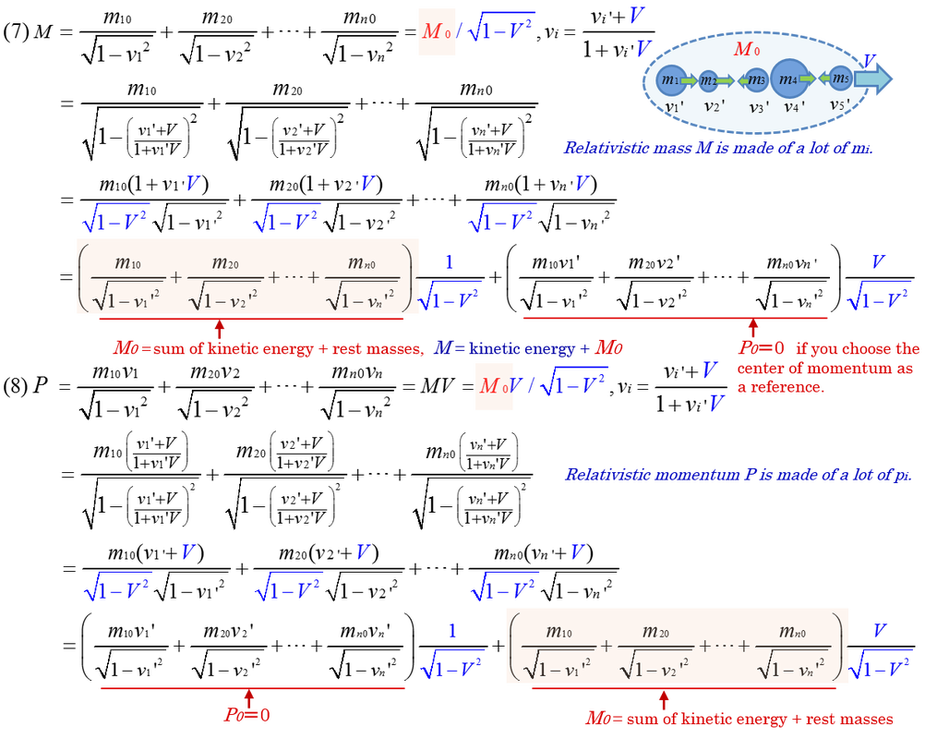
Relativistic mass and its momentum are defined as a vector of Lorentz transformation. Developing this concept, there is
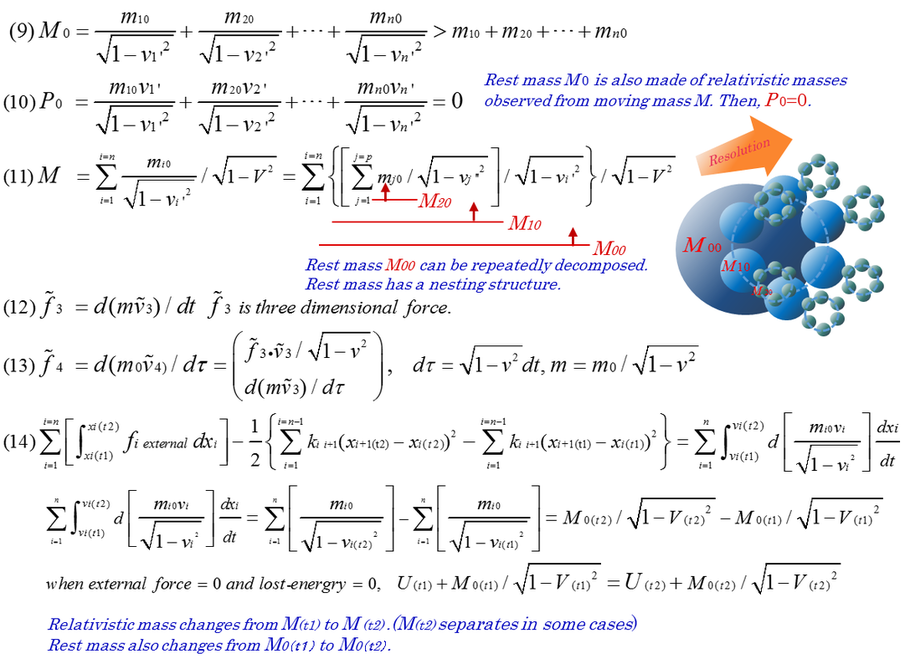
a possibility that a single rest mass is resolved into a group of small moving masses, furthermore, resolved small rest mass is
also repeatedly resolved into smaller moving masses. A single rest mass contains confined kinetic energy. In other words, inner kinetic energy is the composition of rest mass (rest energy). For example, a stationary object is also composed of numerous molecules which have active molecular motion by thermal energy. This energy of confined motion is a part of rest mass. The procedure of decomposition of the molecules means that rest mass of the molecules is resolved into moving atoms which contain kinetic energy and rest mass.
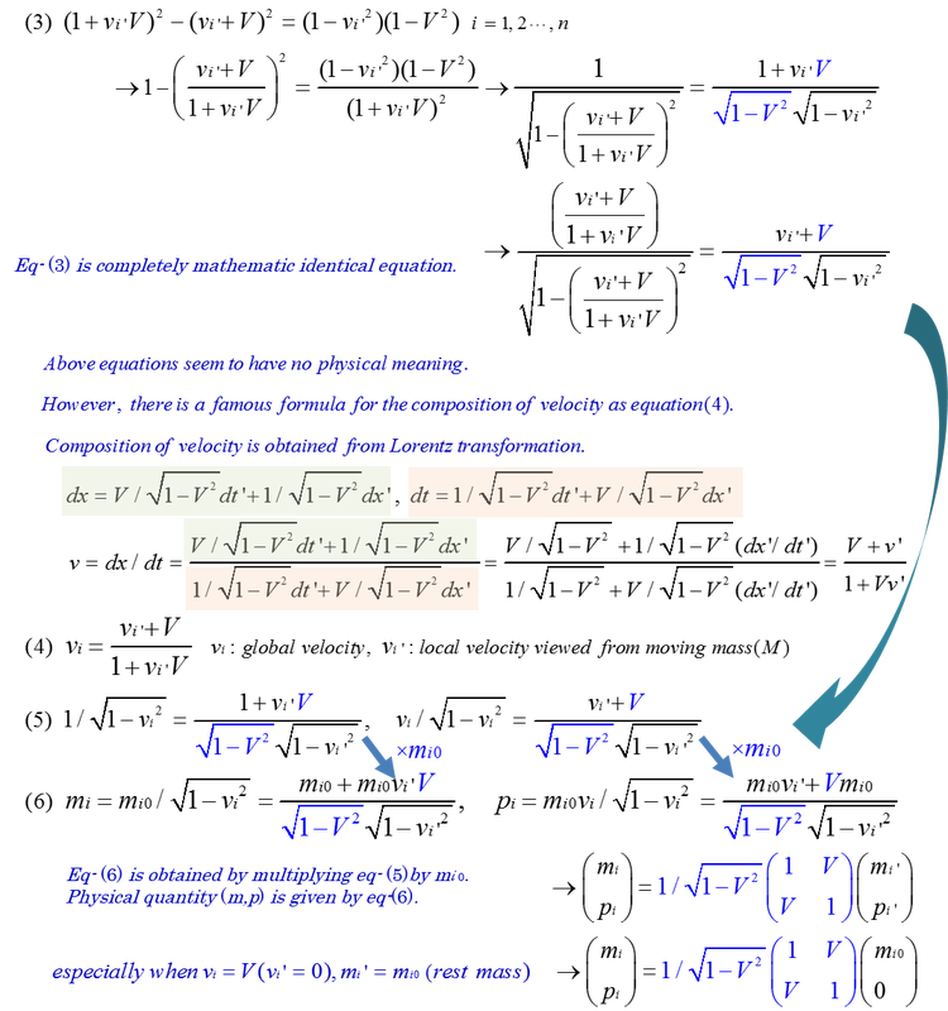
Lorentz transformation of mass and momentum can be applied to a group of moving masses. The application to a group of masses mathematically leads to the fact that rest mass contains inner kinetic energy and consists of a lot of relativistic masses.
dated June 20th, 2012
the latest rev. March 28th, 2020
Preface
Many people get confused about the concept of rest mass in the theory of Special Relativity.
Scientists have deliberated over a rest mass (Gary Oas1, L.B.Okun2 , Max Jammer3).
A single rest mass has been thought to be equivalent to rest energy because relativistic mass is divided into rest mass
and kinetic energy according to Taylor expansion. However, there remains a question on what rest mass is. This article aims
to indicate the concept of rest mass. The common definition that rest mass is the observed mass with no kinetic energy is not
complete. A group of moving masses with arbitrary velocity also forms an equivalent rest mass.
Relativistic mass and its momentum are defined as a vector of Lorentz transformation. Developing this concept, there is
a possibility that a single rest mass is resolved into a group of small moving masses, furthermore, resolved small rest mass is
also repeatedly resolved into smaller moving masses. A single rest mass contains confined kinetic energy. In other words, inner kinetic energy is the composition of rest mass (rest energy). For example, a stationary object is also composed of numerous molecules which have active molecular motion by thermal energy. This energy of confined motion is a part of rest mass. The procedure of decomposition of the molecules means that rest mass of the molecules is resolved into moving atoms which contain kinetic energy and rest mass.
Lorentz transformation of mass and momentum can be applied to a group of moving masses. The application to a group of masses mathematically leads to the fact that rest mass contains inner kinetic energy and consists of a lot of relativistic masses.
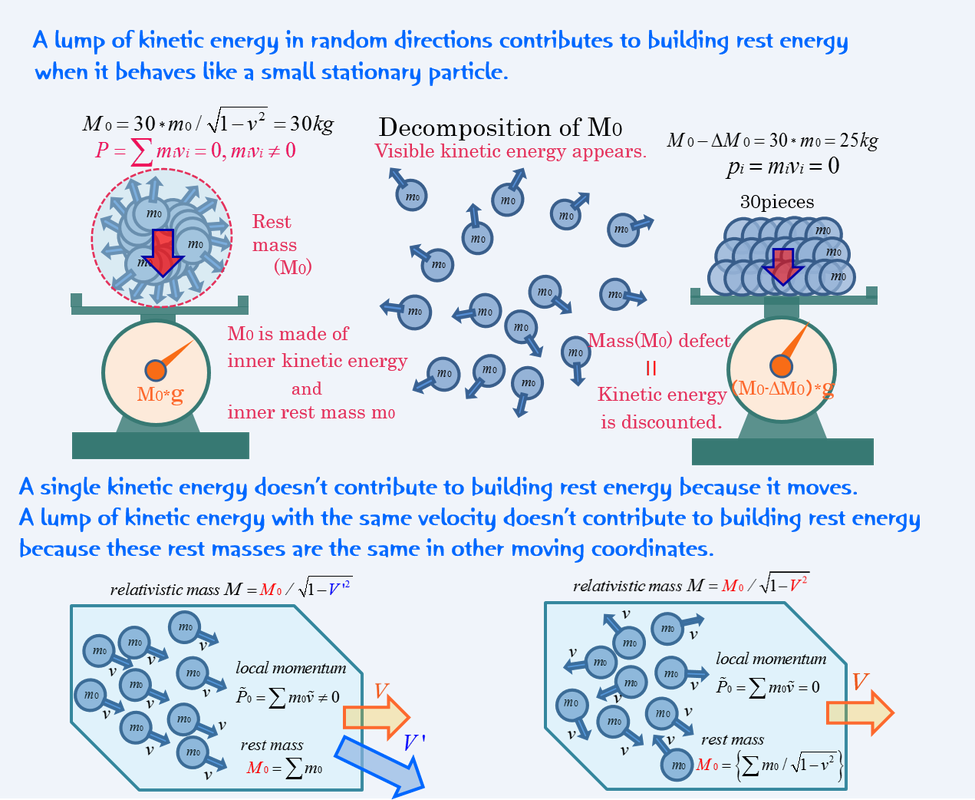
Evidence that rest mass contains kinetic energy
A pair of vertical inner momentum builds a rest mass
Rest mass made of a lot of relativistic masses
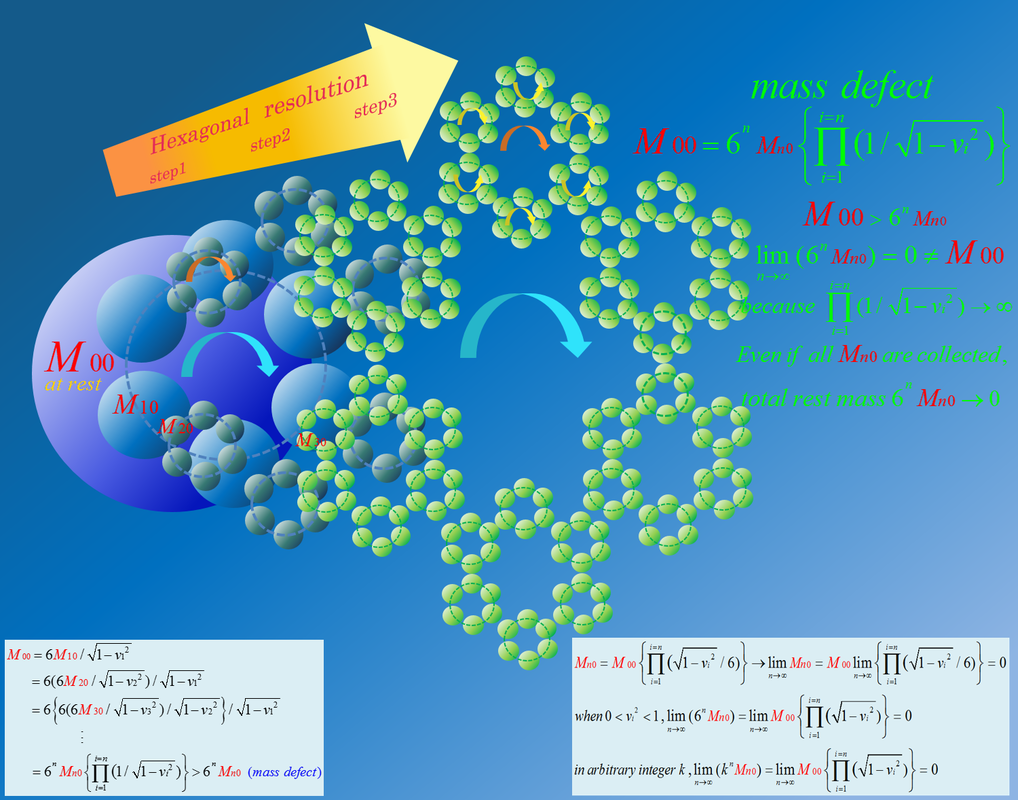
Hexagonal resolution of rest mass(M00) Refer to appendix 9 in page 6.
Summary of essential equations
Contents
1. Preparation for modeling of a group of mass
2. Application of Lorentz transformation for a group of mass
3. Extension of the theory to x-y-z three dimensional space
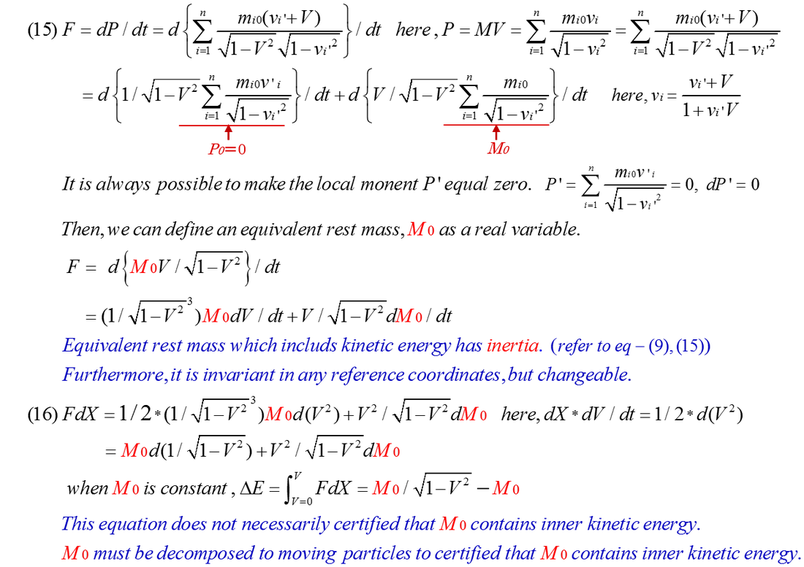
4. Increase of energy in the system is equal to increase of mass in case of free particles (dE=dM=FdX)
5. Modification of F=dP/dt=d(MV)/dt in the theory of special relativity
6. Resolution of rest mass
7. Existence of stationary object in Minkowski space-time
8. E=M=P in case of light
9. Conclusion
10. Postscript
11. Appendix 1 ( Proper time )
12. Appendix 2 ( Lorentz contraction )
13. Appendix 3 ( Time dilation )
14. Appendix 4 ( Spherical light wave )
15. Appendix 5 ( Accelerated motion in special relativity )
16. Appendix 6 ( Variation of relativistic energy observed from different inertial frames )
17. Appendix 7 ( Introduction of relativistic mass's formula )
18. Appendix 8 ( The difficulty of concept of rest energy in Newtonian mechanics )
19. Appendix 9 ( Exponential summation of zero rest mass )
20. Appendix 10 ( Transmission of momentum in one dimensional object )
21. Appendix 11 ( Four-vector expression by Lorentz transformation in t-x-y dimension )
22. Appendix 12 ( Lorentz contraction of distance between moving objects )
23. Appendix 13 ( Increase of inertia caused by the excitation of inner kinetic energy )
24. Appendix 14 ( Time dilation between moving coordinates A and moving coordinates B )
25. Appendix 15 ( Concept of mass defect in special relativity )
26. Appendix 16 ( Relativistic Tsiolkovsky rocket equation in case of constant momentum )
27. Appendix 17 ( Calculation of motion of a mass including inner potential energy )
28. Appendix 18 ( Transverse light velocity in moving coordinates )
29. Appendix 19 ( Compression and expansion of elastic continuum in Minkowski space-time )
30. Appendix 20 ( Different time dilation ratio due to the confusion about Minkowski x-y-t space )
31. Appendix 21 ( Equivalent rest mass composed of twin masses with vertical inner motion to x-axis )
32. Appendix 22 ( An example that rest mass is composed of many relativistic masses in x-y-t space )