What is rest mass? Brief analysis to make it clear that rest mass has kinetic energy
Nobuo Miyaji in
Tokyo Japan
(Dated: June 20th,2012) Welcome your comment
Many pepole get confused about the
concept of rest mass in the theory of Special Relativity. Scientists have also deliberated
over a rest mass.(Gary Oas1, L. B. Okun2 , Max Jammer 3).
A single rest mass has been thought to be equivalent to
rest energy
because relativistic mass is devided into rest mass and
kinetic energy according to Taylor expansion.
However, there remains a
question on what is rest mass. This article aims to
indicate the concept of rest mass. A
group of
moving mass with arbitrary velocity also has
an equivalent rest mass. A group of mass and its momentum are defined as a
vector of Lorentz
transformation. Developing this concept, there is a possibility that a
single
rest mass is resolved into a group
of small rest mass , furthermore, its small rest mass is also repeatedly resolved into smaller mass. A
single rest mass
contains
confined kinetic energy. In orther words, inner kinetic energy is the composition of rest energy.
For
example, a stationary object
is also composed of numerous molecules which have active molecular
motion by thermal
energy. This energy of confined motion is a part of rest mass.
When
we consider photon, we cannot see the light resting because light speed
is maximum. All of the photon energy can be
attributed to momentum
not to rest energy. Rest mass of a certain object except for photon can
be observed if we can
pursue it and see it resting. In this case , we
can say its macro momentum is zero because its position is not moving.
However,we must remenber inner part
of rest mass has momentum in the micro world. If the total of
momentum of micro
world is zero in our stationary coordinate ,
observer considers it to be resting. According to this idea, it
can be proved that
rest mass has kinetic energy by mathematical analysis.
Modeling of a group of mass
At first, a single mass is moving with velocity in a certain inertial coordinate A. 
Relativistic mass (wikipedia.org/wiki/Mass in special relativity4)m is well known as equation(1).
Including momentum p, m and p are expressed by matrix equation(2).
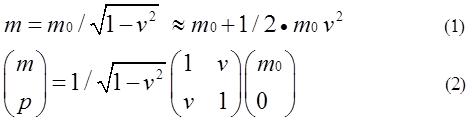
m0 is a rest mass and v is the velocity
of the center of a rest mass in a coordinate
A. v is defined as non-dimensional velocity divided by light speed. Equation
(1),(2) are important to express that m has kinetic energy and rest energy m0.
In addition, m0 is transformed into m according to Lorentz
transformation. However, there remains a basic question about what is rest
energy. When we observe a moving mass m at the same velocity v, m0 is
stationary. Even if the center of rest mass system is resting, it should be
considered that inner part of rest mass is not resting.
To make it
clear what is rest mass, it is possible to suppose that a lot of mass are moving
in a coordinate A as shwon in Fig.2. Among a group, mi
is a mass and vi is the velocity of mass in the preceding coordinate
A.
Gneralized
application of Lorentz transformation.
Mass and momentum are expressed by follwing expression
in the coordinate A


A group of mass is observed
from a diferent coordinate B. Coordinate
B is moving with velocity V in the coordinate A. There is always a coordinate
where a group of mass is considered to be stationary. According to the
formula of synthesis of velocity, vi is converted into vi’ in the coordinate B. Velocity
vi’ is expressed by equation (5). Using equation
(5), mi’ and pi’ are expressed by equation (6),(7).
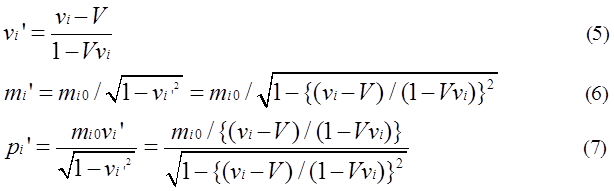
Equation (8) is always true. 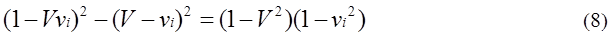
By substituting equation (3),(4),(8) into
equation (6), (7), equation (9), (10) are obtained.
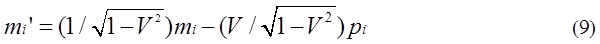
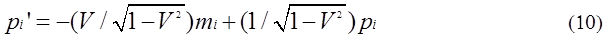
The sum of mi
and pi are expressed by following equations.
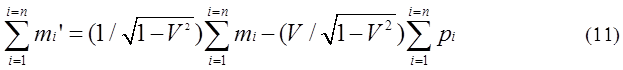
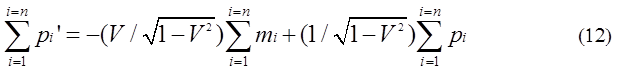
A group of mass
and momentum are defined as following.
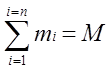
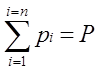
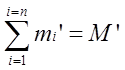
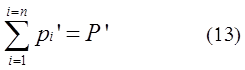
Equations (11),
(12) are expressed by a matrix equation.
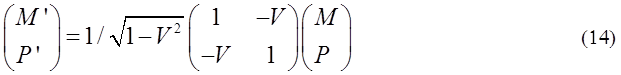
Equation (14) is exactly Lorentz transformation of a group of mass and
momentum similar to the fundamental equation (2).
This equation implies that a
group of mass has an invariant as a rest mass as well as a sigle mass. A group
of mass becomes a rest mass when its momentum P' is zero in coordinate B.
When we choose a coordinate B which makes P’ equal zero, P=MV is obtained from the second line equation
of matrix equation (14). Using the relation of P=MV, the first line equation of matrix equation (14) is
following.
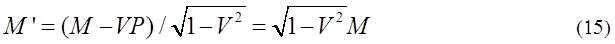
Refering to
the relation P=MV, equation (16) is obtained. M’ can be considered as an equivalent rest mass M0.
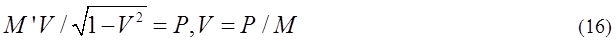
From equation (6) and equation(13), equivalent rest mass M’
is larger than the total of rest mass mi0. Despite the fact that
mi' is moving, M' is considered to be staionary in coordinate B which makes P’ equal zero.
Equation(18) indicates a sigle mass m has an invariant. Equation(19) also means a group of mass M has an invarinat.
Only when a group of rest mass is confined within M0,
M0
has an invariant in any reference system.
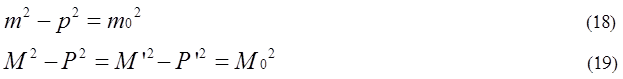
In considering
a rest mass, it is not a mathematical point but a compound of smaller
particles which contain kinetic energy and rest energy. And then,
resolved rest energy of smaller particles has also kinetic energy and
rest energy.
Conclusion
Mathematical
analysis concerning a group of rest mass and momentum helps to understand the
concept of rest mass.
1) A group of mass and a group of momentum can
be defined as a vector of Lorentz transformation. Furthermore, the
velocity of a group of mass can be decided, and the moment of a group
of mass is converted to zero in the moving
coordinate with the velocity
2) Equivalent
rest mass M0 is larger than the total of inner rest mass. That means
confined kinetic energy is the composition
of rest energy.
3) There
is a possibility that a single rest mass can be infinitively resolved into a group of small mass by repeated procedures
of resolution.
<Postscript>
We can imagine an extreme case. The smallest rest mass may
be composed of two photons with symmetrical momentum
in a certain
coordinate. The origin of rest mass may be photon energy 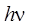 which is attributed to electromagnetic field energy.
which is attributed to electromagnetic field energy.
<reference>
1 Gary Oas, On the abuse and
use of relativistic mass,
physics.ed-ph 21 Oct 2005 p1-2
2 LL. B. Okun (1989), "The Concept of Mass", Physics Today 42 (6): p31–36
3 Max Jammer (1997), Concepts of Mass in Classical and
Modern Physics, Courier Dover
Publications, p179, ISBN 0486299988
4 http://en.wikipedia.org/wiki/Mass_in_special_relativity


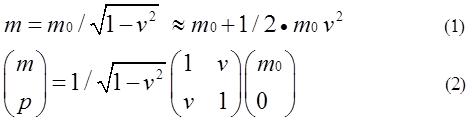


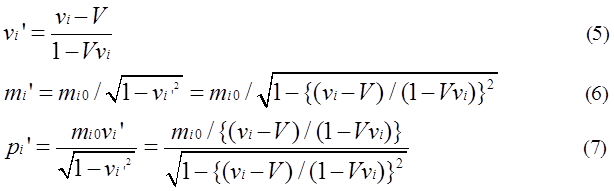
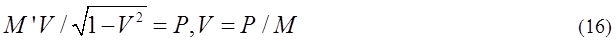
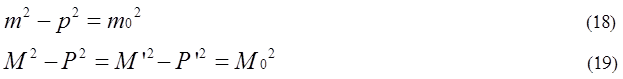
 which is attributed to electromagnetic field energy.
which is attributed to electromagnetic field energy.