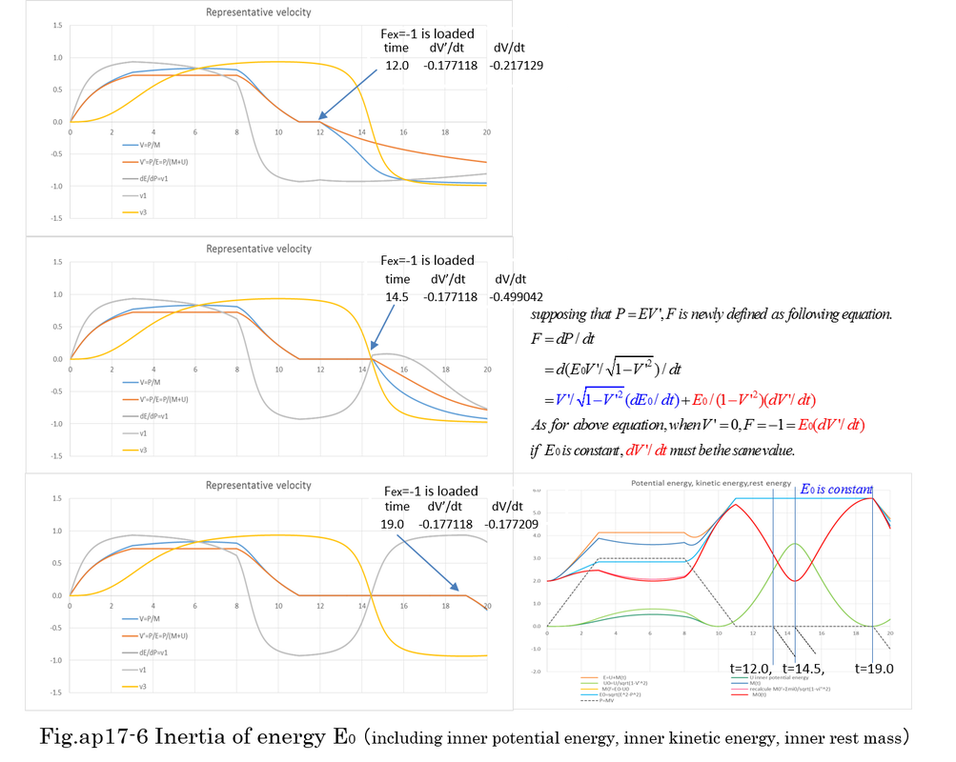
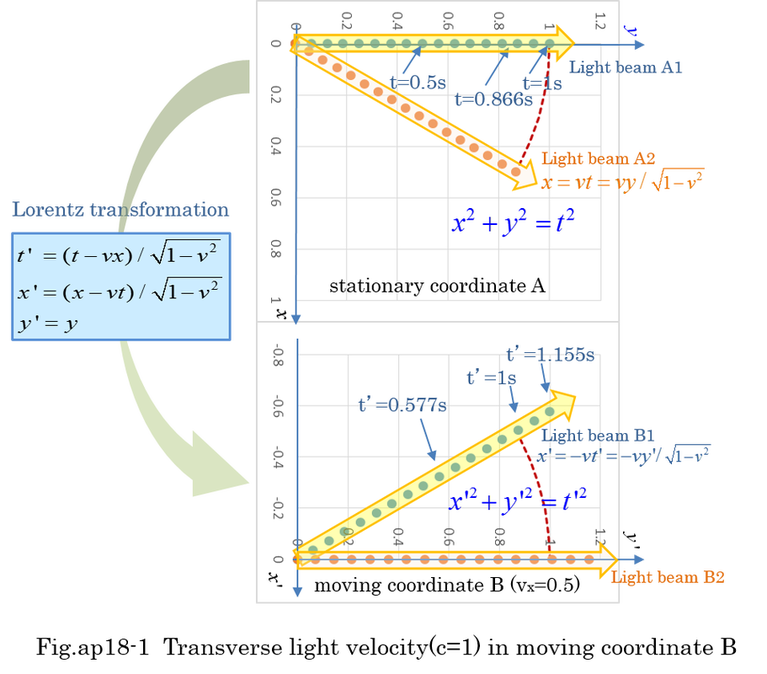
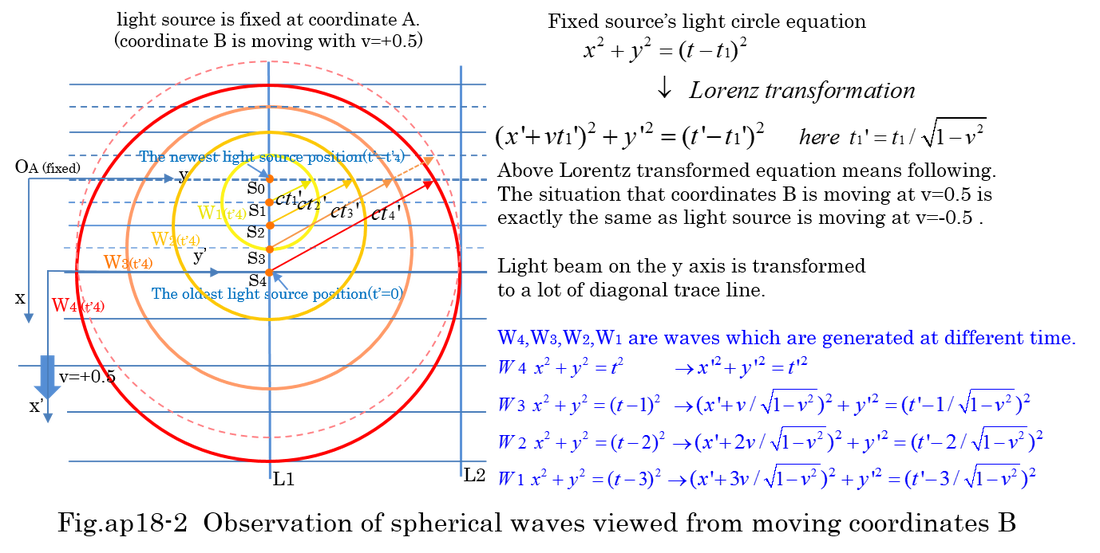
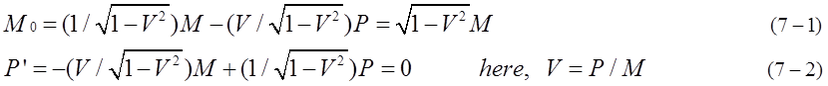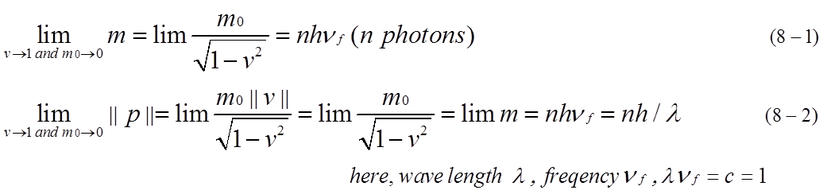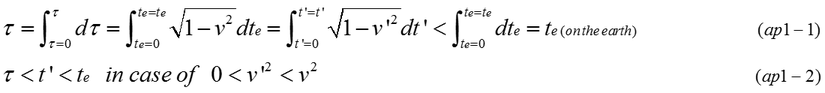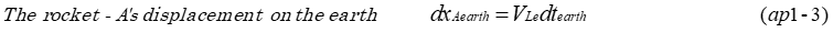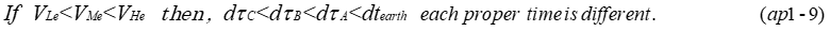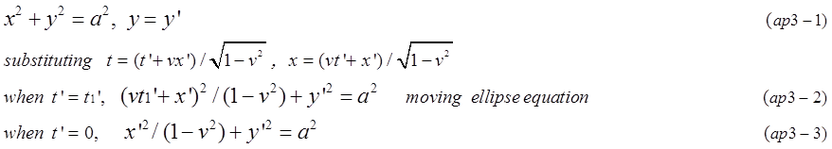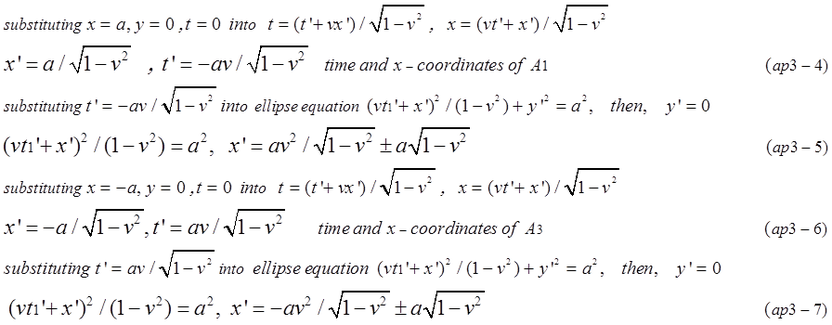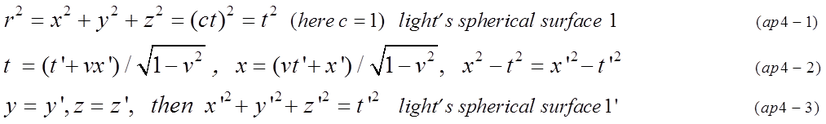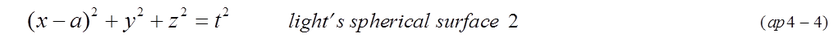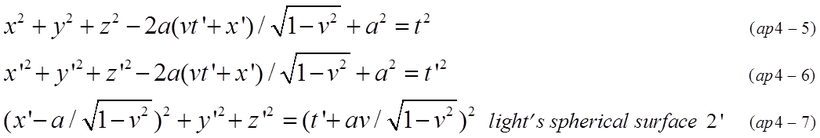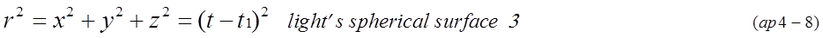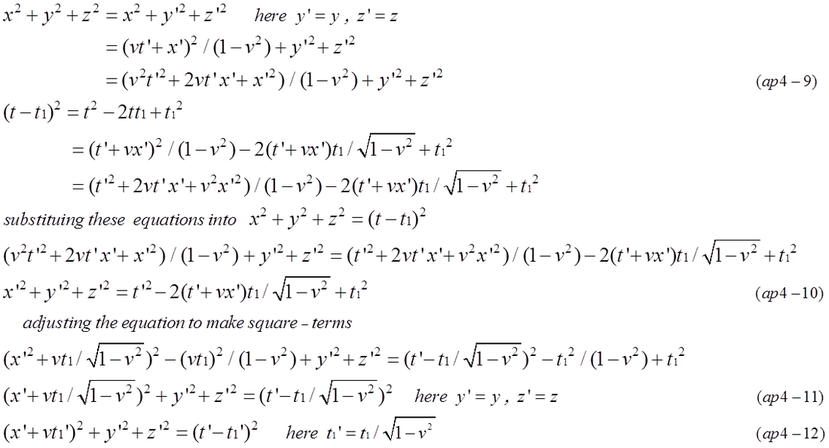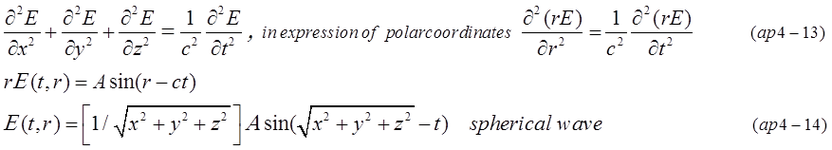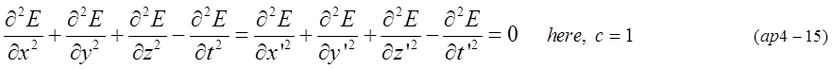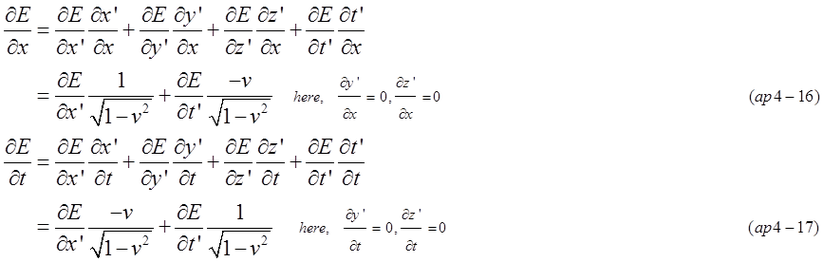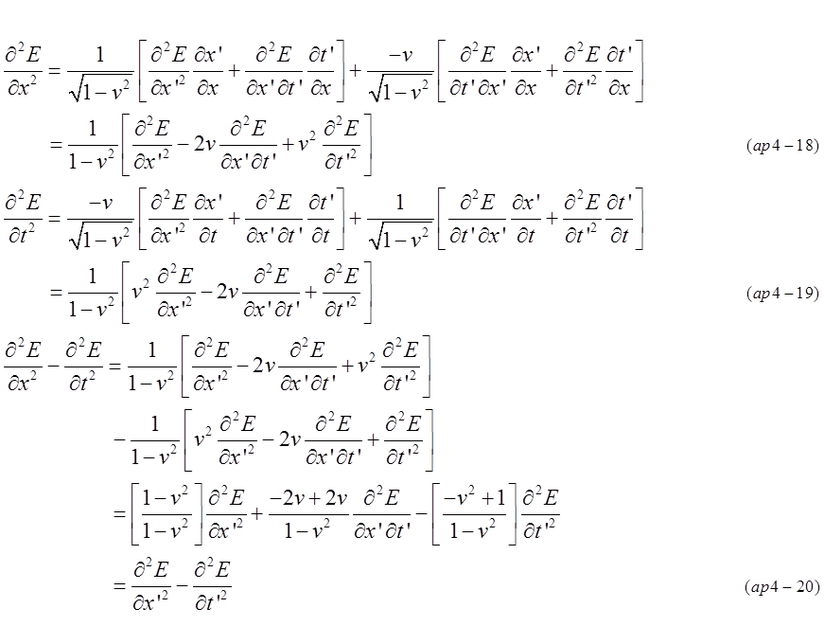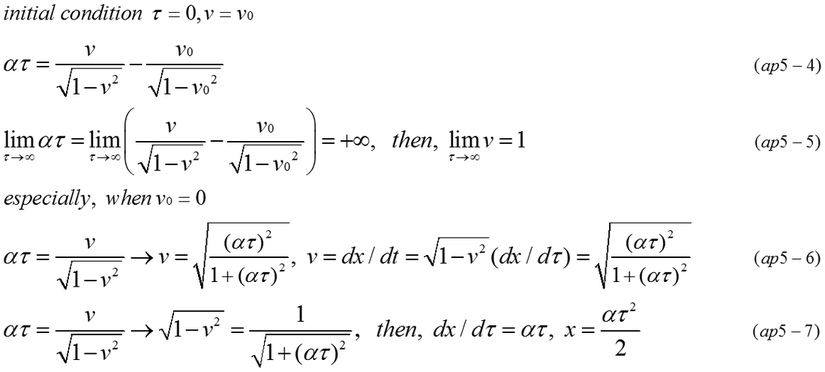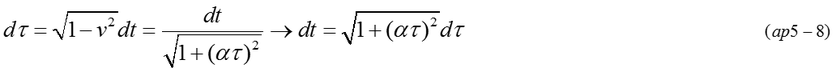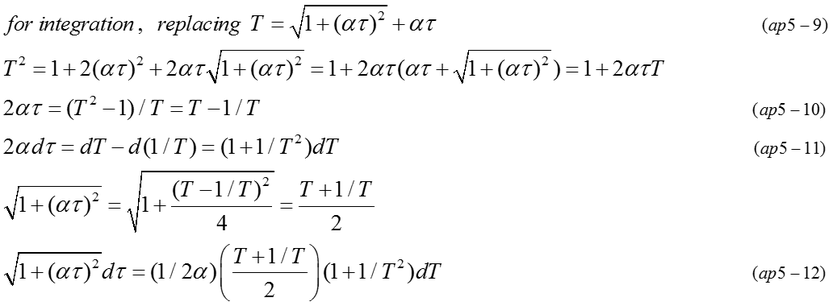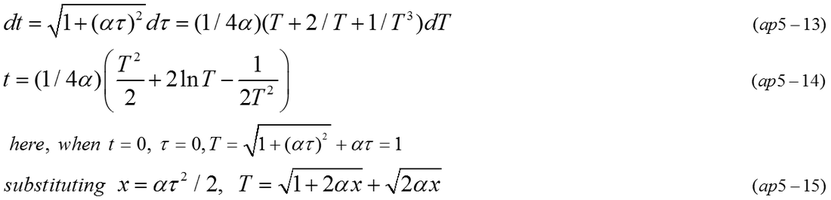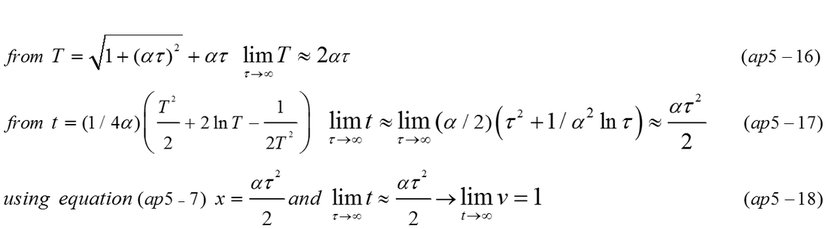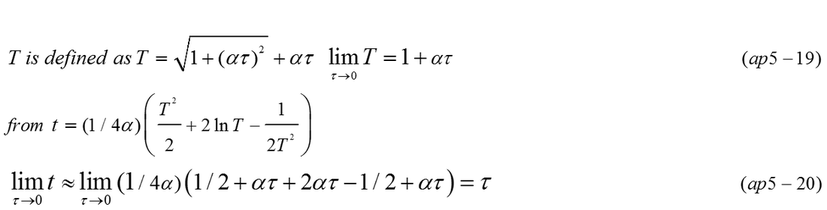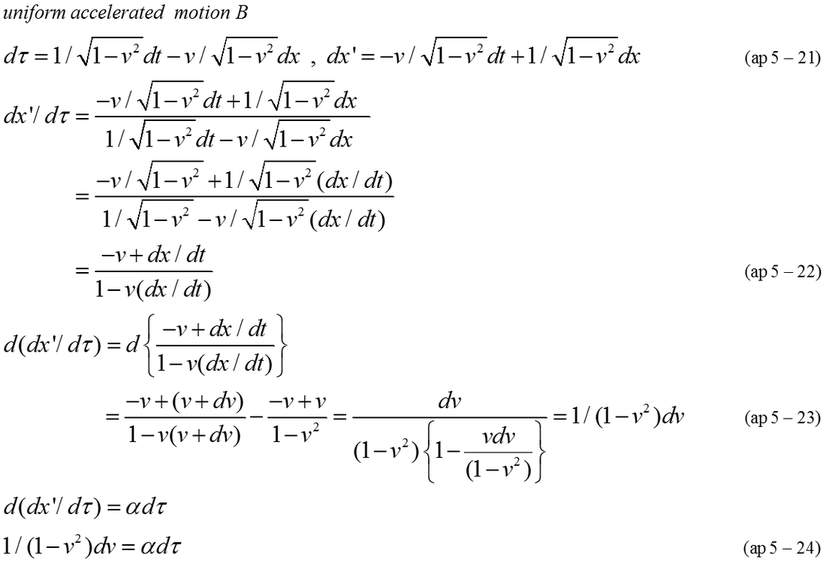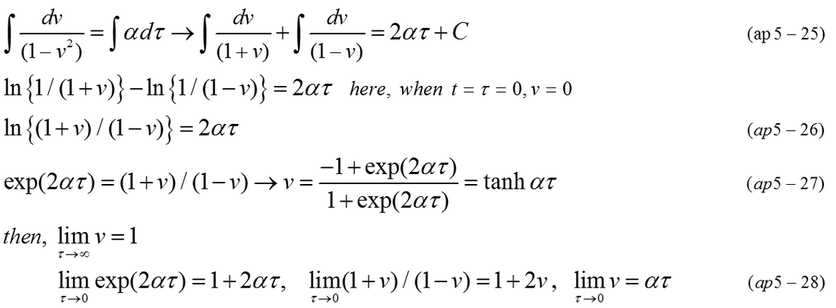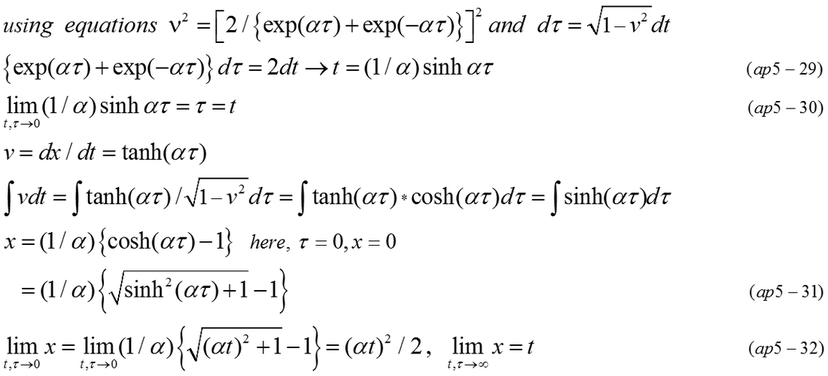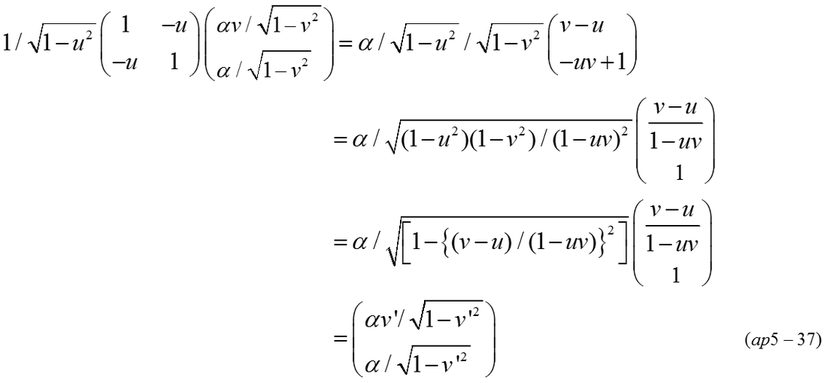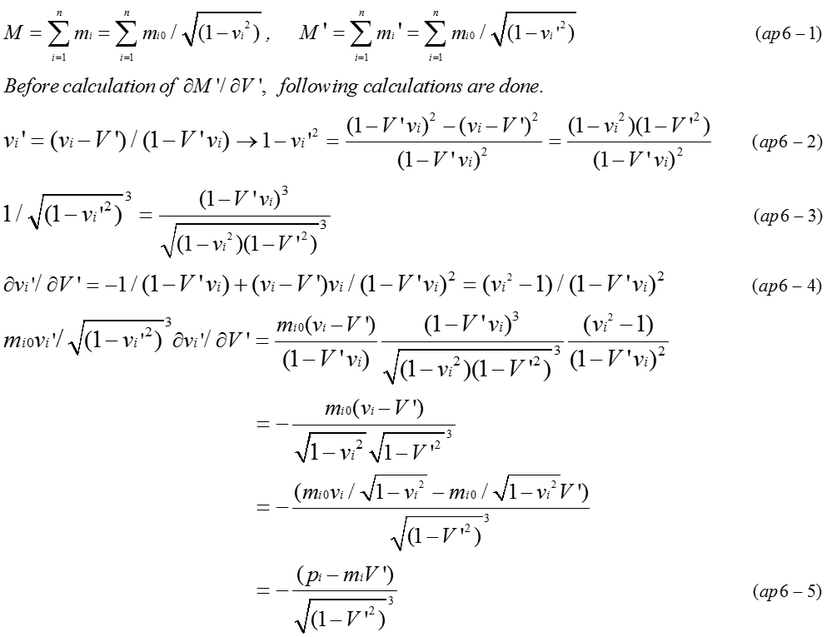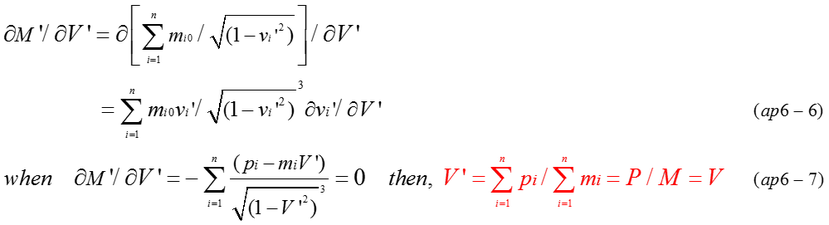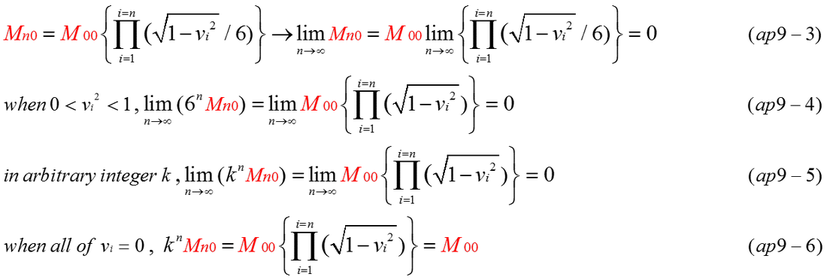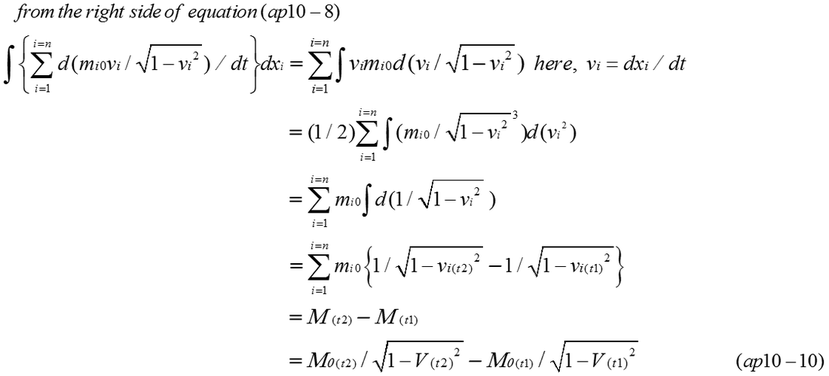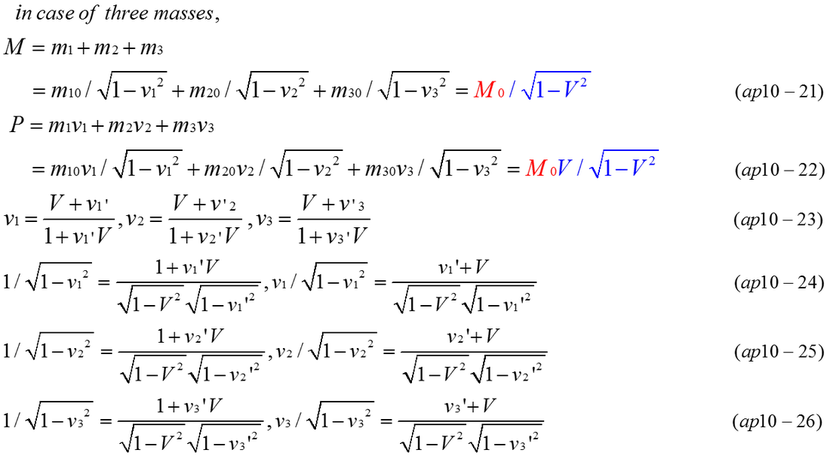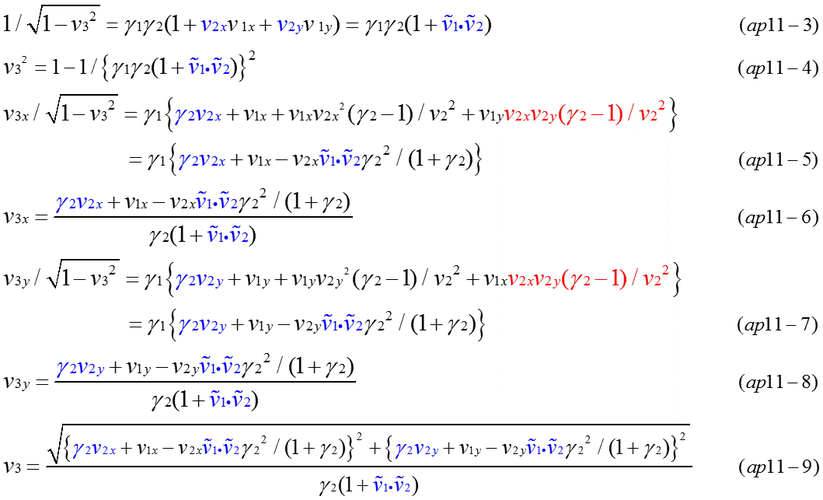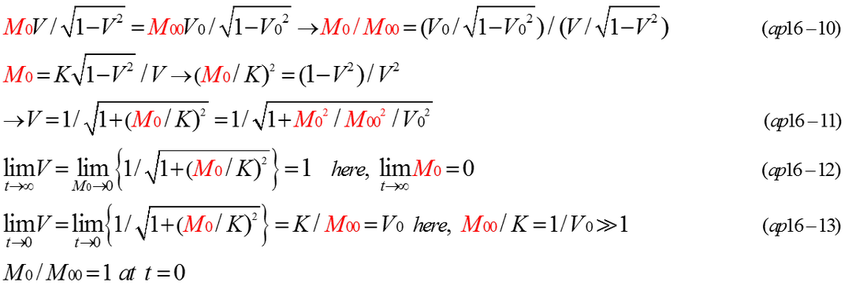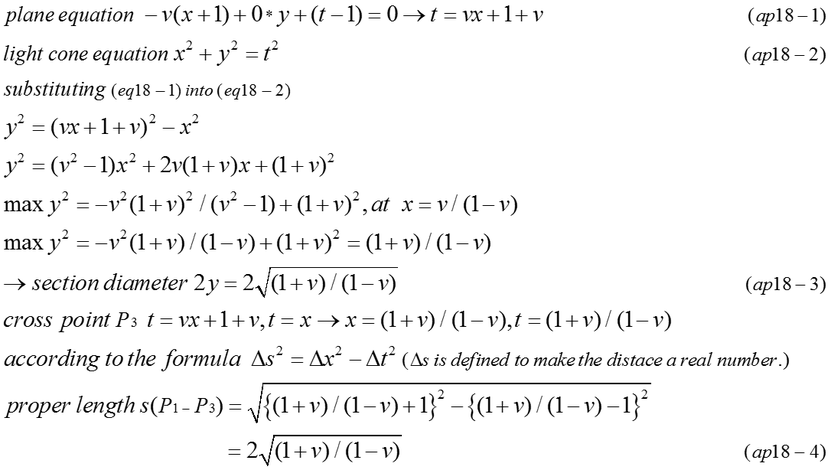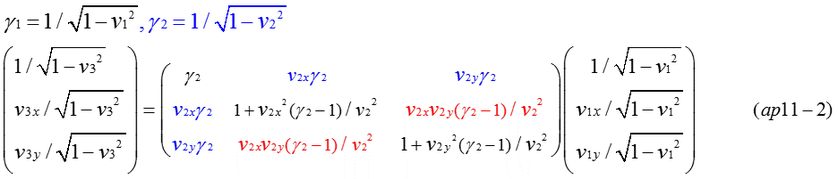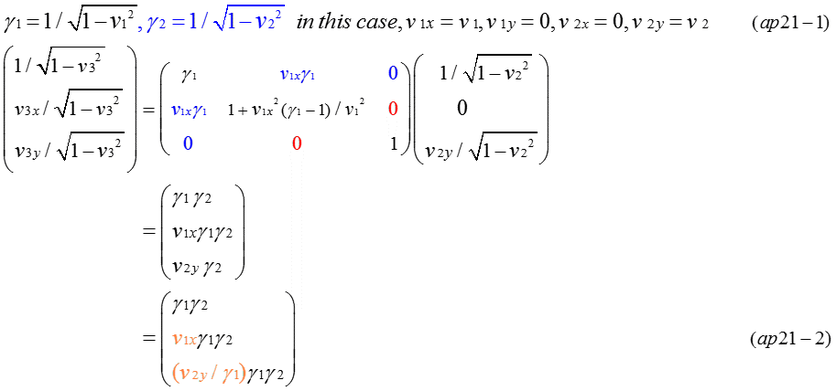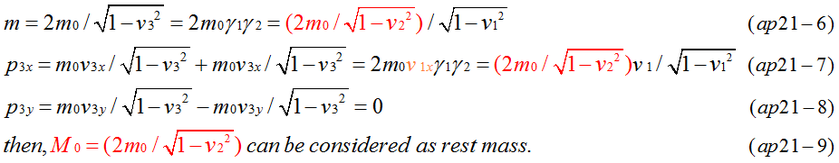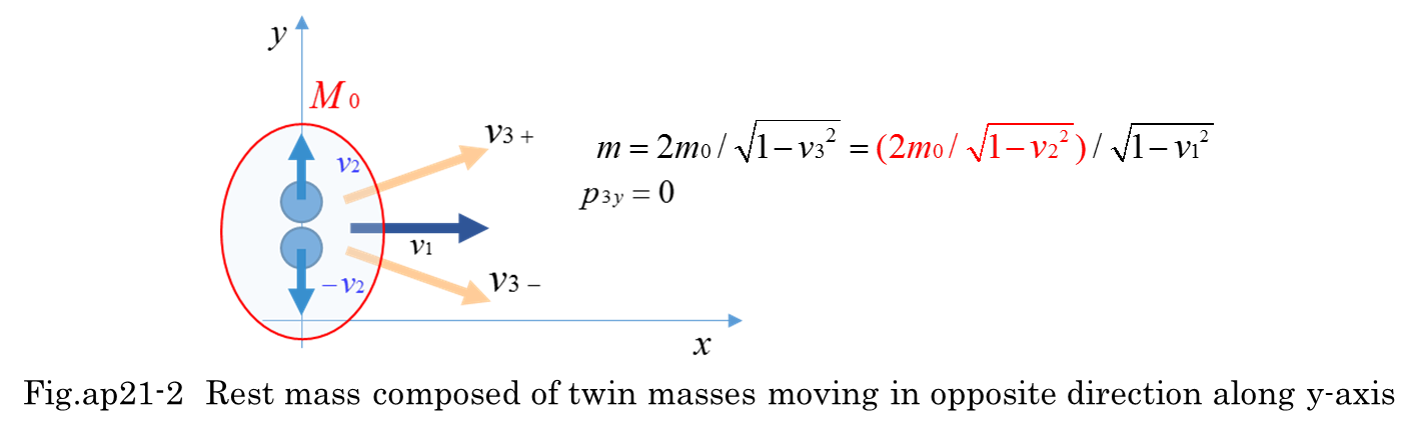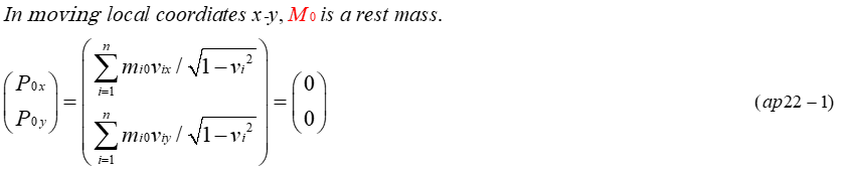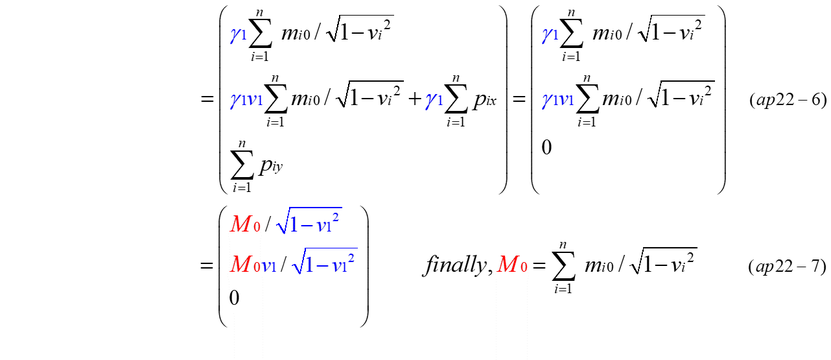6. Resolution of rest mass
In considering a rest mass, it is not a mathematical point but a compound of small particles which contain kinetic energy
and rest energy. Repeating procedures of resolution of mass, resolved rest energy of smaller particles has also kinetic energy and rest energy. Equation (6-1) indicates that M has three levels of hierarchy. Of course, countless times of resolution is possible. Partial summation of mijk comes together as equations (6-2,6-3). Furthermore, partial summation of mij comes together as equation (6-4,6-5).
In considering a rest mass, it is not a mathematical point but a compound of small particles which contain kinetic energy
and rest energy. Repeating procedures of resolution of mass, resolved rest energy of smaller particles has also kinetic energy and rest energy. Equation (6-1) indicates that M has three levels of hierarchy. Of course, countless times of resolution is possible. Partial summation of mijk comes together as equations (6-2,6-3). Furthermore, partial summation of mij comes together as equation (6-4,6-5).
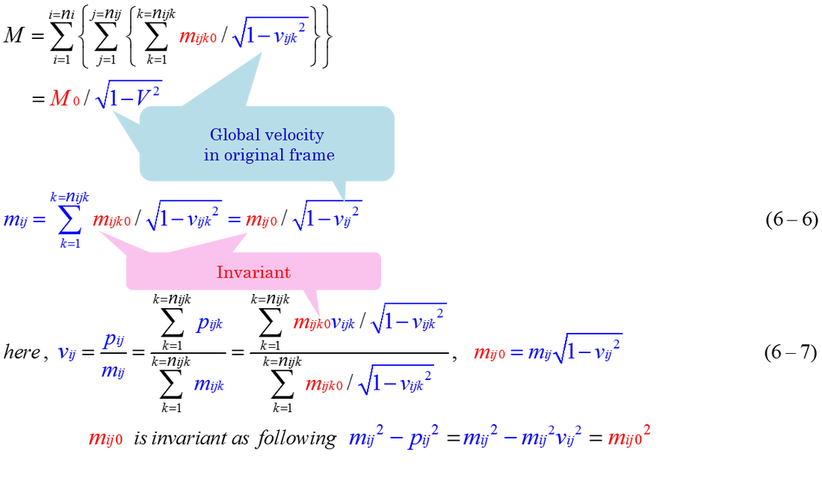
Equation (6-6) indicates relations between relativistic mass, invariant (rest mass) and global velocity. Blue color variables are global in original coordinates. Red color variables are invariants in any inertial coordinates.
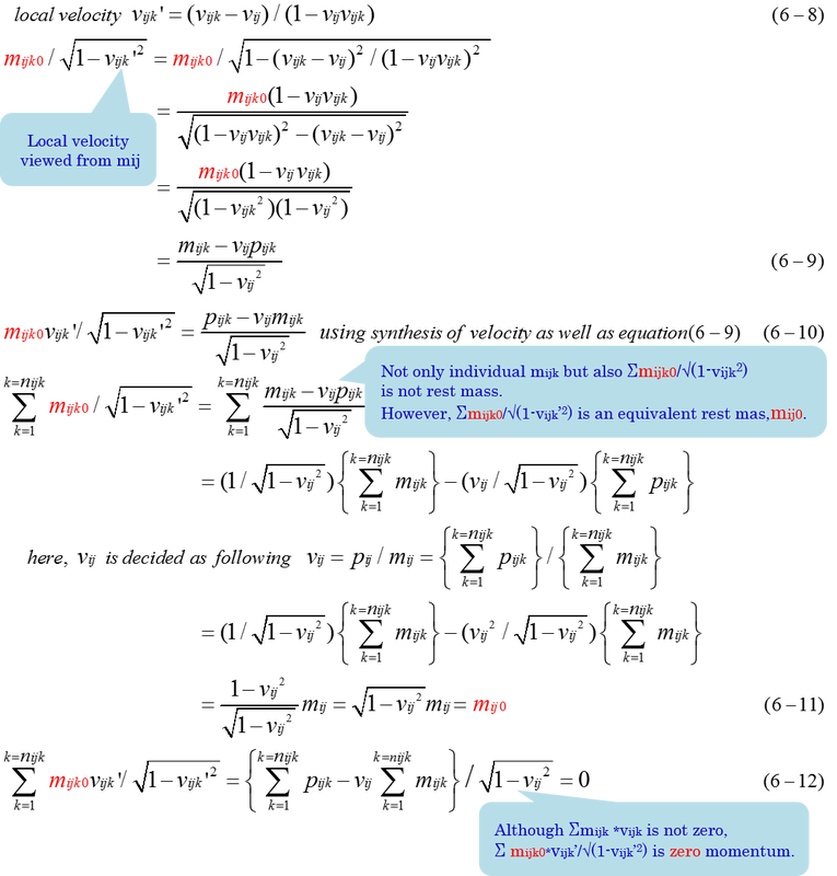
Following equations shows the procedure of grouping of rest mass. Local velocity is expressed by global velocity as equation (6-8). Local velocity(vijk') is the velocity observed from the center of momentum of mij. Individual mijk0/sqrt(1-vijk'^2) is expressed by equation (6-9). It is not mijk. Summation of mijk0/sqrt(1-vijk'^2) is mij0. Needless to say, summation of mijk=mijk0/sqrt(1-vijk^2) is mij.
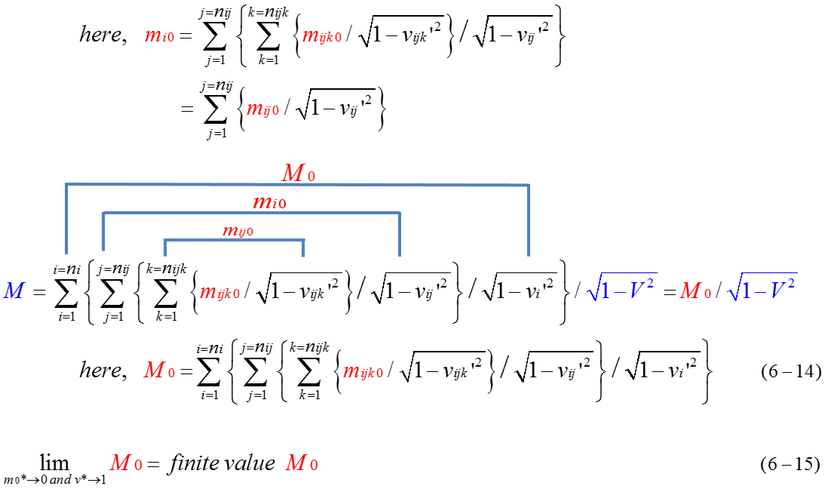
As it is explained, relativistic mass(M) is expressed by the triple summation of mijk(=mijk0/sqrt(1-vijk^2). However, rest mass(M0) is expressed by invariant(rest mass) and local velocities. We must notice that M0 is not the summation of mi0/sqrt(1-vi^2) but the summation of mi0/sqrt(1-vi'^2). Each mi0 is always invariant in any reference system and it must be observed from the center of the momentum of a group of relativistic mass(mi). If vi' is not the velocity observed from the center of the momentum, the summation of mi0/sqrt(1-vi'^2) can not be equal to rest mass(M0). Each mij0 is also invariant, and it must be observed from the center of the momentum of mass mi0. As to mijk0, it must be observed in the same way.
In equation (6-15), m*0 and v* mean many of the ultimate values of rest mass and velocity. M0 is expected to be much larger than the total of ultimate rest mass(m*0) because velocity(v*) is close to 1(light speed). M0 is larger than the total of rest mass( triple summation of mijk0) because of the factor(1/sqrt(1-v^2)).
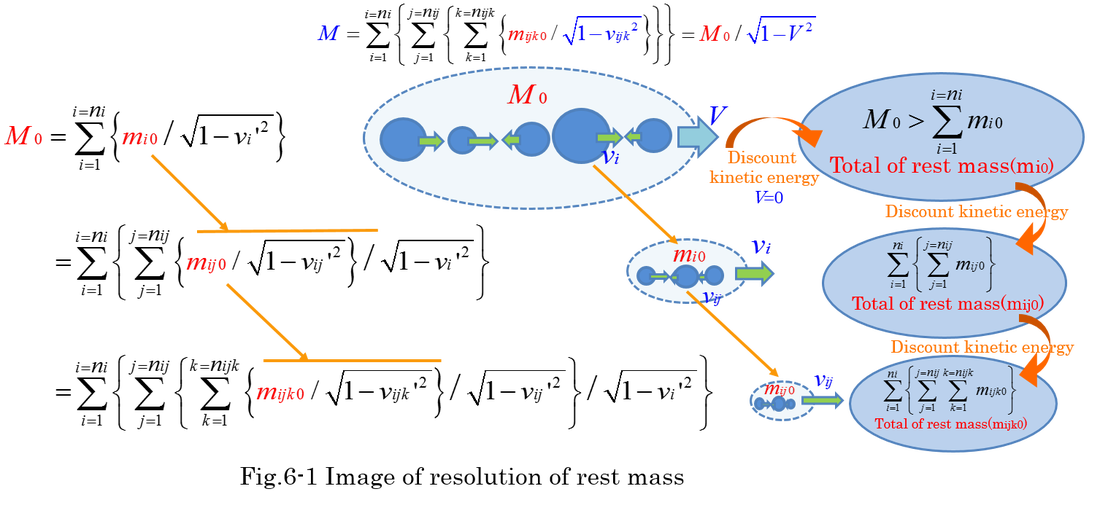
There is a hierarchy within M0 as shown in Fig.6-1. Supposing the separation of the rest mass(M0) by external force,
it is easy to imagine mass defect. Confined kinetic energy is released as visible kinetic energy. Total of small rest mass
is less than M0 because of the release of inner kinetic energy. If the object is deeply destructed, separation of rest mass
reaches smaller mass. When the number of smaller mass is very large, and the factor(1/sqrt(1-v^2)) is enormous, inner
kinetic energy no longer constitutes the original rest mass. This phenomenon can be called mass defect. A part of original
rest mass is surely lost because released energy mi0/sqrt(1-vi'^2) is estimated as rest mass mi0. It looks like material partially disappears. However, mass defect only indicates that inner kinetic energy is released and turns to visible kinetic energy.
We know energy conservation is kept because kinetic energy of small particles is released or photon energy(E=pc) such as gamma radiation appears. Kinetic energy appears by the separation of materials. Nuclear fission is typical phenomenon. In addition, heat energy often appears from the solid material in ordinary chemical reaction.
There is a hierarchy within M0 as shown in Fig.6-1. Supposing the separation of the rest mass(M0) by external force,
it is easy to imagine mass defect. Confined kinetic energy is released as visible kinetic energy. Total of small rest mass
is less than M0 because of the release of inner kinetic energy. If the object is deeply destructed, separation of rest mass
reaches smaller mass. When the number of smaller mass is very large, and the factor(1/sqrt(1-v^2)) is enormous, inner
kinetic energy no longer constitutes the original rest mass. This phenomenon can be called mass defect. A part of original
rest mass is surely lost because released energy mi0/sqrt(1-vi'^2) is estimated as rest mass mi0. It looks like material partially disappears. However, mass defect only indicates that inner kinetic energy is released and turns to visible kinetic energy.
We know energy conservation is kept because kinetic energy of small particles is released or photon energy(E=pc) such as gamma radiation appears. Kinetic energy appears by the separation of materials. Nuclear fission is typical phenomenon. In addition, heat energy often appears from the solid material in ordinary chemical reaction.
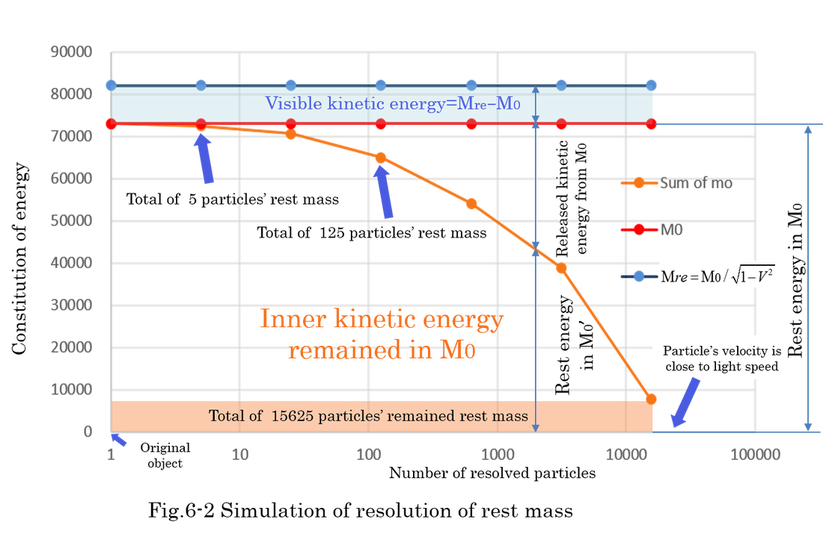
Fig.6-2 indicates the result of simulation of rest mass. Calculation is done according to equation (6-1).
At first, the object is supposed to be composed of 15625 particles with arbitrary rest mass and velocity. Random numbers
generate to make particle's velocity close to 1 or close to -1 for 15625 particles. Although calculation process reverses the way of resolution, the object is divided by 5 particles. Then, each of 3125 larger particles has rest mass. This means 5 times of resolution. As the second step, each 3125 particles is divided into 625 particles. This means 4 times of resolution. When continuing these procedures up to one particle (corresponding to the original object), total of relativistic mass is conserved because it expresses total energy in coordinate A. However, the total of rest mass is different in each procedure of resolution of rest mass. Original rest mass(M0) is largest because it contains inner kinetic energy. Although the result of this calculation is based on the simple resolution of rest mass M0, Fig.6-2 indicates that the summation of 15625 particles' rest mass is only 10% of rest mass(M0). When the object consists of a large number of high speed particles, what is so-called material is mainly made of a lot of kinetic energy or momentum.
At first, the object is supposed to be composed of 15625 particles with arbitrary rest mass and velocity. Random numbers
generate to make particle's velocity close to 1 or close to -1 for 15625 particles. Although calculation process reverses the way of resolution, the object is divided by 5 particles. Then, each of 3125 larger particles has rest mass. This means 5 times of resolution. As the second step, each 3125 particles is divided into 625 particles. This means 4 times of resolution. When continuing these procedures up to one particle (corresponding to the original object), total of relativistic mass is conserved because it expresses total energy in coordinate A. However, the total of rest mass is different in each procedure of resolution of rest mass. Original rest mass(M0) is largest because it contains inner kinetic energy. Although the result of this calculation is based on the simple resolution of rest mass M0, Fig.6-2 indicates that the summation of 15625 particles' rest mass is only 10% of rest mass(M0). When the object consists of a large number of high speed particles, what is so-called material is mainly made of a lot of kinetic energy or momentum.
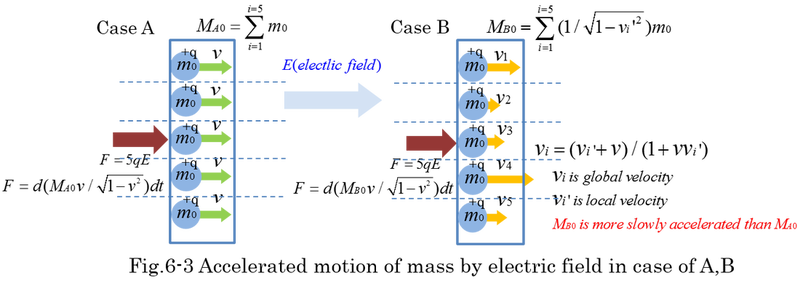
Inertia of rest mass(M0) is expected to be different from the summation of m0 when M0 consists of a lot of relativistic mass(mi). It is possible that individual motion of mass is calculated separately. However, to clear the concept of group of mass, two cases of accelerated motion are considered. Fig.6-3 indicates that M0 is accelerated by electric field. Each rest mass is equally m0 and it has electric charge(+q). In case of B, vi' is local velocity in the center of momentum of MB0. It is supposed that the initial velocity(PA/MA) of MA0 and that (PB/MB) of MB0 are the same. vi' has positive or negative value. The force(5q*E) is equally generated by electric field(E). Repulsion of q+ is supposed to be shielded by some metal screens. Equation (6-16) indicates that rest mass of group of m0 is MA0=5m0. Considering the momentum of MB0, Equation (6-18) is obtained from equation (6-17). Equation (6-18),(6-19),(6-20) indicates that rest mass of group of randomly moving m0 is MB0=Σm0/sqrt(1-vi'^2). Even if the initial velocity is the same, MB0 is more slowly accelerated than MA0. MB0 is not constant during the acceleration of mass because there is no constraint between individual mass.
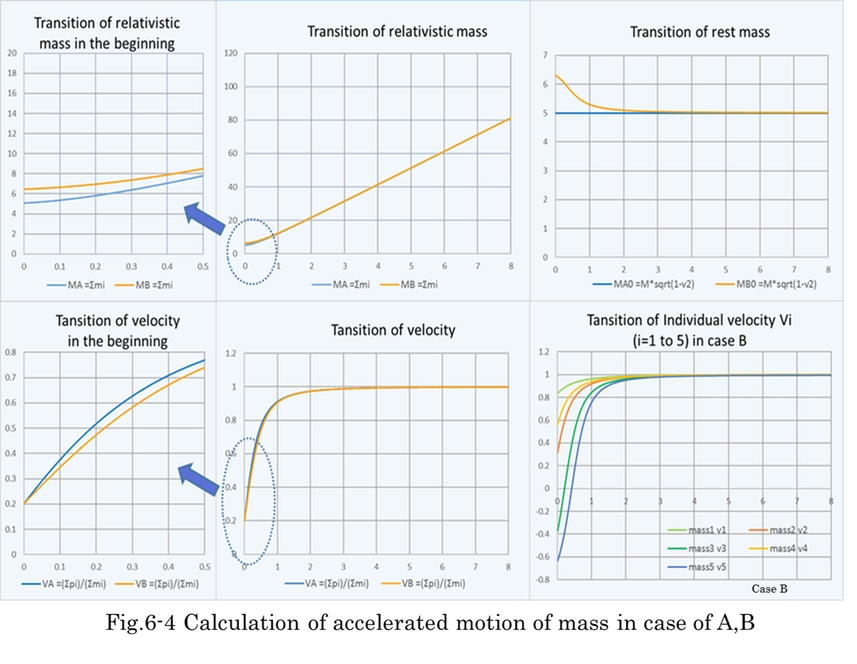
Fig.6-4 is a simulation of case A and case B. Following is the condition of simulation. m0=1 (constant), F=Eq=1, VA=VB=0.2 at time=0 although vi is random. The result of calculation indicates that velocity is accelerated up to light speed both in case A and case B. In the beginning, rest mass in case B is larger than case A because local velocity is random. For that reason, there is a little difference of velocity between two cases in the beginning of acceleration. In case B, individual velocity comes to light velocity. Rest mass of case B approaches rest mass of case A because all the velocities come to coincide.
To avoid misunderstanding of resolution of mass, it is appropriate to give the reverse case like electrolysis of water. Decomposition of mass does not always decrease the total of rest mass. Hydrogen gas and oxygen gas are produced by adding electric energy. The total of rest mass of gas molecule is larger than the rest mass of water. In this case, inner kinetic energy which is derived from potential energy is increased by electric energy through the electrolysis of water.
7. Existence of stationary object in Minkowski space-time
We must recognize that a certain object is not a mathematical point but a physical substance. Even if the object is at rest,
it has inner momentum and rest mass. Although rest mas can be resolved into arbitrary momentum and smaller rest mass,
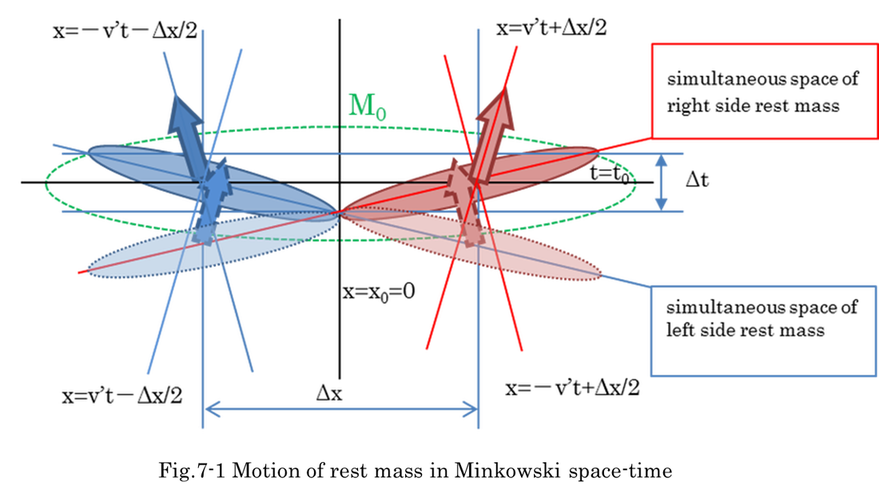
it can be supposed that a stationary object is virtually resolved into two symmetrical moving substances shown in Fig.7-1.
The right side velocity is v', the left side velocity is -v' when observing two substances from the center of M0. These resolved masses do not exist in the same space-time because the momentum is symmetric. Total momentum of the
object is zero due to the reciprocal motion. The necessity of reciprocal motion might be unnatural because the
mechanism for confinement of motion is not solved.
We must recognize that a certain object is not a mathematical point but a physical substance. Even if the object is at rest,
it has inner momentum and rest mass. Although rest mas can be resolved into arbitrary momentum and smaller rest mass,
it can be supposed that a stationary object is virtually resolved into two symmetrical moving substances shown in Fig.7-1.
The right side velocity is v', the left side velocity is -v' when observing two substances from the center of M0. These resolved masses do not exist in the same space-time because the momentum is symmetric. Total momentum of the
object is zero due to the reciprocal motion. The necessity of reciprocal motion might be unnatural because the
mechanism for confinement of motion is not solved.
Fig.7-1 indicates the motion of a pair of rest mass in Minkowski space-time. Here, the distance between the center of
two substances is Δx, and the length of substance generates the difference of time Δt in the space-time of coordinates A.
We can only measure the position and the momentum in different time. Rest mass(rest energy) exists for the period of Δt.
We are liable to assume that rest mass M0 has rest energy at the particular time of t and it exists at the position of x.
In fact, rest energy exists between t-Δt/2 and t+Δt/2. In the same way, it exists between x0-Δx/2 and x0+Δx/2. Rest mass
continues existing in such condition for a long time. This might be related to Heisenberg uncertainty principle. Decisive
momentum and position of an infinitively small particle will make it difficult to understand uncertainty principle. Probabilistic
theory for the existence of a particle can be avoidable. It seems intrinsically incapable to measure the exact position of
mass and momentum at the same time.
two substances is Δx, and the length of substance generates the difference of time Δt in the space-time of coordinates A.
We can only measure the position and the momentum in different time. Rest mass(rest energy) exists for the period of Δt.
We are liable to assume that rest mass M0 has rest energy at the particular time of t and it exists at the position of x.
In fact, rest energy exists between t-Δt/2 and t+Δt/2. In the same way, it exists between x0-Δx/2 and x0+Δx/2. Rest mass
continues existing in such condition for a long time. This might be related to Heisenberg uncertainty principle. Decisive
momentum and position of an infinitively small particle will make it difficult to understand uncertainty principle. Probabilistic
theory for the existence of a particle can be avoidable. It seems intrinsically incapable to measure the exact position of
mass and momentum at the same time.
Furthermore, equation (7-1),(7-2) indicates V(=P/M) is the same and M0 is also the same as long as M and P are the same.
In other words, even if inner kinetic energy of M0 is partially different, observed mass (total energy) M and momentum P
are the same. We must know the way of virtual resolution is arbitrary. When rest mass is M0, its resolved rest mass
and momentum have degree of freedom to some extent. In equation (6-1), there are many degrees of freedom.
Combination of different mi and different vi gives the same rest mass M0.This might be also related to Heisenberg
uncertainty principle.
In other words, even if inner kinetic energy of M0 is partially different, observed mass (total energy) M and momentum P
are the same. We must know the way of virtual resolution is arbitrary. When rest mass is M0, its resolved rest mass
and momentum have degree of freedom to some extent. In equation (6-1), there are many degrees of freedom.
Combination of different mi and different vi gives the same rest mass M0.This might be also related to Heisenberg
uncertainty principle.
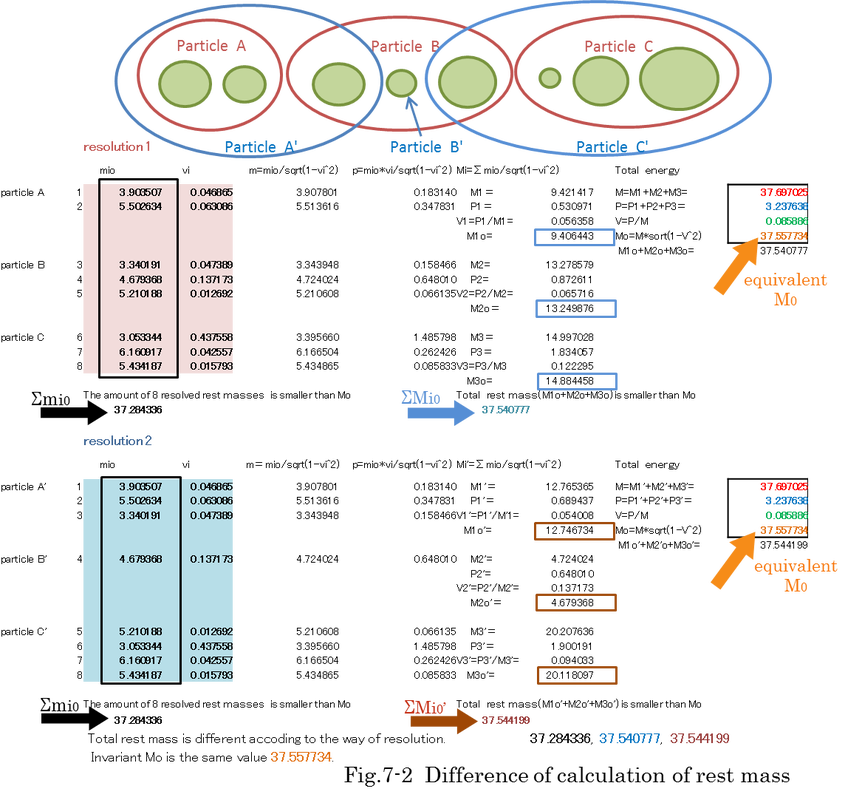
Fig.7-2 indicates an example of simulation. Calculation table in Fig.7-2 indicates that the amount of rest mass is different
according to the way of resolution. As shown in Fig.7-2, a group of moving mass consists of 8 particles, and it is resolved
into three particles in two different ways. However, invariant mass M0 and relativistic mass M are kept as the same value
because total energy is kept constant. When the measurement of its mass and momentum are done, we cannot
confirm which part of mass is completely measured because these particles cannot exist stationarily at the same time in
Minkowski space-time. It is necessary to reconsider the definition of particle.
according to the way of resolution. As shown in Fig.7-2, a group of moving mass consists of 8 particles, and it is resolved
into three particles in two different ways. However, invariant mass M0 and relativistic mass M are kept as the same value
because total energy is kept constant. When the measurement of its mass and momentum are done, we cannot
confirm which part of mass is completely measured because these particles cannot exist stationarily at the same time in
Minkowski space-time. It is necessary to reconsider the definition of particle.
8. E=m=P in case of light
When the velocity of mass approaches to light speed (v=1), m0/0 becomes infinity. However, it is possible to define an idealized limit of m0/0 when m0 is close to zero. Then, m and p are expressed by equation (8-1),(8-2). Rest mass
m0 approaches to zero. However, we must notice that m is not zero, but a finite value. m might be photon energy and
it exactly changes to p (EMAN physics homepage 6). If a group of mass can be resolved indefinitely, M and M0 can be resolved into summation of momentum. Even if the summation of rest mass approaches zero, M and M0 have a finite value.
Rest mass is a lump of energy or momentum which is not moving from here to there in a certain inertial frame. Center of rest mass is not moving, but divided parts of rest mass are moving. It might be doubtful that something called material exists other than energy or momentum.
When the velocity of mass approaches to light speed (v=1), m0/0 becomes infinity. However, it is possible to define an idealized limit of m0/0 when m0 is close to zero. Then, m and p are expressed by equation (8-1),(8-2). Rest mass
m0 approaches to zero. However, we must notice that m is not zero, but a finite value. m might be photon energy and
it exactly changes to p (EMAN physics homepage 6). If a group of mass can be resolved indefinitely, M and M0 can be resolved into summation of momentum. Even if the summation of rest mass approaches zero, M and M0 have a finite value.
Rest mass is a lump of energy or momentum which is not moving from here to there in a certain inertial frame. Center of rest mass is not moving, but divided parts of rest mass are moving. It might be doubtful that something called material exists other than energy or momentum.
The following equation (8-3) is not proved. If ultimate mass m* consists of photon energy, there will be enormous inner
photons like standing wave with various frequency in the mass of M0. Ultimate result of equation (6-1) will be equation (8-3).
Each of velocity vi,vj,vk....does not need to approach 1. However, the velocity of light mass is almost close to 1 because
light mass is easy to move. When equation (8-3) is supposed to be an infinite product, M0 will diverge into infinity because each element of 1/sqrt(1-vi^2)>1. For this reason, equation (8-3) must be a finite product even if the summation of photon energy is very small. Each photon energy has not rest mass, however, the summation of photon has a rest mass and zero momentum. The frequency of photons could be distributed from zero to a certain value.
If we consider the rest mass of our universe, going to an extreme case, M0 could be the total rest mass of the universe.
photons like standing wave with various frequency in the mass of M0. Ultimate result of equation (6-1) will be equation (8-3).
Each of velocity vi,vj,vk....does not need to approach 1. However, the velocity of light mass is almost close to 1 because
light mass is easy to move. When equation (8-3) is supposed to be an infinite product, M0 will diverge into infinity because each element of 1/sqrt(1-vi^2)>1. For this reason, equation (8-3) must be a finite product even if the summation of photon energy is very small. Each photon energy has not rest mass, however, the summation of photon has a rest mass and zero momentum. The frequency of photons could be distributed from zero to a certain value.
If we consider the rest mass of our universe, going to an extreme case, M0 could be the total rest mass of the universe.
9. Conclusion
Mathematical analysis concerning a group of rest mass and momentum helps to understand the concept of rest mass.
1) A group of mass and a group of momentum can be defined as a vector of Lorentz transformation. Furthermore, the velocity
of a group of mass can be decided, and the momentum of a group of mass is converted to zero in the moving coordinate
with the velocity.
2) Equivalent rest mass M0 is larger than the total of inner rest mass. This means that confined kinetic energy of inner rest
mass is the composition of rest mass M0 ( rest energy ).
3) There is a possibility that a single rest mass can be infinitively resolved into a group of small mass by repeating procedures
of resolution. All physical objects (including elementary particles) which have rest mass might have inner structure.
10. Postscript
We can imagine an extreme case. Although there is no evidence, the smallest rest mass may be composed of some photons with symmetrical momentum in a certain coordinate. The origin of rest mass may be photon energy which is
attributed to electromagnetic field energy.
Even if the total of resolved rest mass approaches zero, the rest mass of a group of mass is not zero. In other words,
the mass of object has finite value because the velocity of the smallest resolved mass approaches light speed (v=1).
Mathematical analysis concerning a group of rest mass and momentum helps to understand the concept of rest mass.
1) A group of mass and a group of momentum can be defined as a vector of Lorentz transformation. Furthermore, the velocity
of a group of mass can be decided, and the momentum of a group of mass is converted to zero in the moving coordinate
with the velocity.
2) Equivalent rest mass M0 is larger than the total of inner rest mass. This means that confined kinetic energy of inner rest
mass is the composition of rest mass M0 ( rest energy ).
3) There is a possibility that a single rest mass can be infinitively resolved into a group of small mass by repeating procedures
of resolution. All physical objects (including elementary particles) which have rest mass might have inner structure.
10. Postscript
We can imagine an extreme case. Although there is no evidence, the smallest rest mass may be composed of some photons with symmetrical momentum in a certain coordinate. The origin of rest mass may be photon energy which is
attributed to electromagnetic field energy.
Even if the total of resolved rest mass approaches zero, the rest mass of a group of mass is not zero. In other words,
the mass of object has finite value because the velocity of the smallest resolved mass approaches light speed (v=1).
<Appendix 1 --- Proper time>
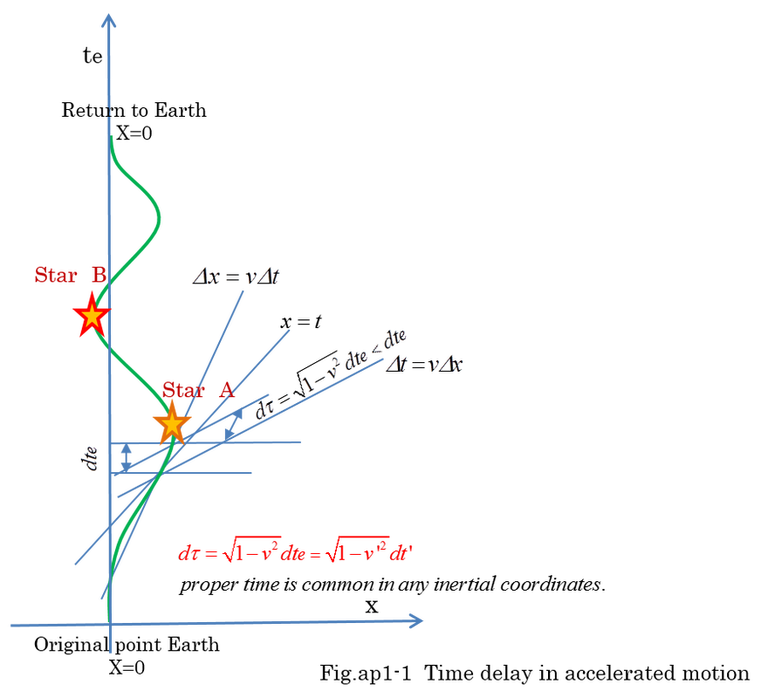
Let you know interesting application of proper time. The proper time which elapsed along with the moving object is the shortest time. There is a famous paradox. Younger brother stays on the earth and older brother travels in the space with acceleration and deceleration, and returns to younger brother with reducing speed. The amount of time elapsed is different between two brothers. Fig.ap1-1 indicates the integration of proper time is shorter than the time younger brother experienced.
This paradox looks like 'Japanese fairy tale of Taro Urashima who had a strange experience that his friends had grown much older when he returned home'. If the earth is supposed to be one of the inertial reference frame in zero gravity, there is no need to refer to the general relativity.
This paradox looks like 'Japanese fairy tale of Taro Urashima who had a strange experience that his friends had grown much older when he returned home'. If the earth is supposed to be one of the inertial reference frame in zero gravity, there is no need to refer to the general relativity.
Equation (ap1-1) indicates that proper time is calculated by knowing the object's velocity v or v' in any reference frame.
We must remember that v and v' is not the velocity of the coordinates but the velocity of the same object observed from different inertial coordinates. When observed velocity v is larger than v', the amount of time elapsed te on the earth is longer than t' in other coordinates. The reason why is that dτ=sqrt(1-v^2)dte=sqrt(1-v'^2)dt' is always satisfied. In this case, we can say infinitesimal proper time, dτ< dt' < dte as shown in equation (ap1-2). We must remember that sqrt(1-v^2)dt is no longer invariant if v is the velocity of object observed from accelerated coordinates. Therefore, when we discuss the proper time(dτ) , the velocity of the object must be measured from inertial coordinates even if the motion of the object is accelerated.
We must remember that v and v' is not the velocity of the coordinates but the velocity of the same object observed from different inertial coordinates. When observed velocity v is larger than v', the amount of time elapsed te on the earth is longer than t' in other coordinates. The reason why is that dτ=sqrt(1-v^2)dte=sqrt(1-v'^2)dt' is always satisfied. In this case, we can say infinitesimal proper time, dτ< dt' < dte as shown in equation (ap1-2). We must remember that sqrt(1-v^2)dt is no longer invariant if v is the velocity of object observed from accelerated coordinates. Therefore, when we discuss the proper time(dτ) , the velocity of the object must be measured from inertial coordinates even if the motion of the object is accelerated.
Proper time of a certain flying object is common in any inertial coordinates and it depends on the velocity of object. if you are on a certain flying object, you will experience the lapse of proper time. However, if you observe flying objects on the earth, you will find proper time of any flying object is shorter than the elapse of time on the earth. But, you don't feel longer time elapse. Your life span may be the same unless you can compare each proper time. Fig.ap1-2 shows proper time of three rockets and each displacement. VLe,VMe,VHe are the velocity of rocket-A,B,C observed on the earth.
dtearth is coordinate time on the earth. dxAearth (the displacement of the rocket-A on the earth) is expressed by equation(ap1-3). Then, executing Lorentz transformation, equation(ap1-5) is obtained using the equation (ap1-3). Matrix (ap1-4) is a Lorentz transformation which converts from the coordinates of the earth to the coordinates of rocket-A. Equations (ap1-5,6,7,8) indicate that proper time τA, τB, τC are obtained from Lorentz transformation.

Though proper time is common in any inertial coordinates, each rocket-A,B,C has different proper time.
As is shown in the equation (ap1-1) and (ap1-5), proper time is obtained by multiplying sqrt(1-v^2) by dt. According to this formula, how is the proper time of rocket-A observed from rocket-B expressed? We already obtained τA. Proper time τAB which is defined as proper time observing rocket-A from rocket-B. Following procedures show τAB=τA. Considering the velocity of the earth is -VMe against the rocket-B, the velocity of rocket-A observed from rocket-B is equation (ap-1-10). Using Lorentz transformation matrix, equations (ap1-11,12) are obtained. Using calculation technique and equation (ap1-11), it is finally proved by procedures of equation (ap1-13) that τAB=sqrt(1-VAB^2)dtB=sqrt(1-VLe^2)dtearth=τA
<Appendix 2 --- Lorentz contraction>
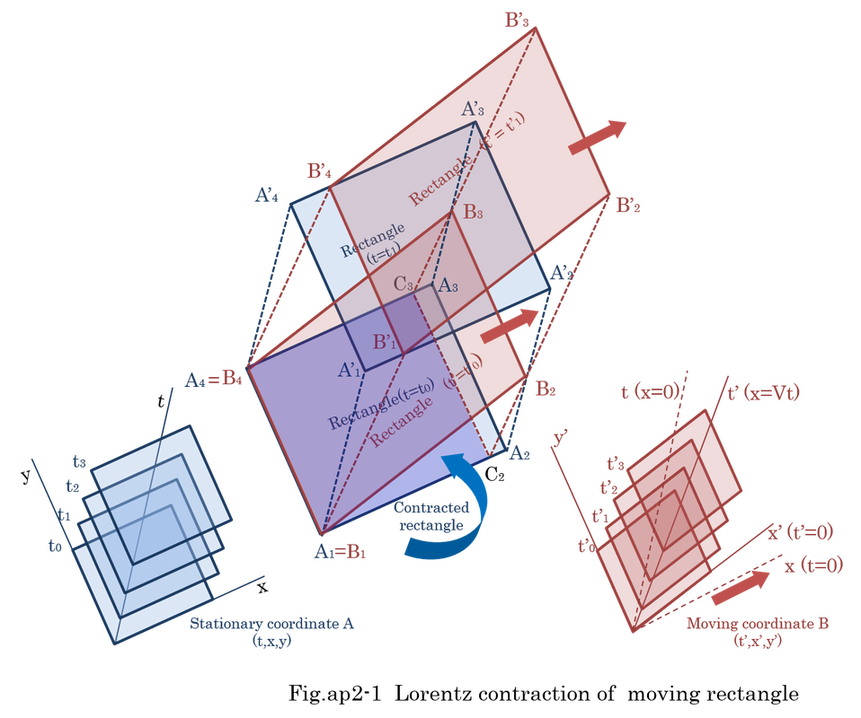
Lorentz contraction is well known in Special Relativity. It does not mean actual contraction of the length in the moving coordinates. Fig.ap2-1 shows the physical meaning of contraction. Supposing that the one rectangle A1A2A3A4 is at rest in coordinates A, and the other rectangle B1B2B3B4 is moving along x axis with the velocity V in coordinates A. These two rectangles are the same size in each coordinates. Coordinates B is moving with velocity V in the coordinates A. Rectangle A'1A'2A'3A'4 and rectangle B'1B'2B'3B'4 are rectangles in the future time. The observer in the coordinates A is liable to consider that all of the points both in rectangle A1A2A3A4 and in rectangle B1B2B3B4 exist in the simultaneous world (t,x,y).
In fact, only rectangle A1A2A3A4 exists in the simultaneous world (t,x,y).
Besides, all the line segments of y and y' axis exist at the same time in coordinates A because y and y' axis are not affected by Lorentz transformation. As shown in Fig.ap2-1, moving rectangle B1B2B3B4 exists over different time of coordinates A.
In general, the length of line segment is defined as the length between two points in the simultaneous world. As a result, moving rectangle B1B2B3B4 is considered to be contracted like rectangle B1C2C3B4. Line segment B1C2 and B4C3 exist at the same time in coordinates A. Then, the observer in the coordinates A considers the length of B1C2 as the length of line segment of rectangle B1B2B3B4
In fact, only rectangle A1A2A3A4 exists in the simultaneous world (t,x,y).
Besides, all the line segments of y and y' axis exist at the same time in coordinates A because y and y' axis are not affected by Lorentz transformation. As shown in Fig.ap2-1, moving rectangle B1B2B3B4 exists over different time of coordinates A.
In general, the length of line segment is defined as the length between two points in the simultaneous world. As a result, moving rectangle B1B2B3B4 is considered to be contracted like rectangle B1C2C3B4. Line segment B1C2 and B4C3 exist at the same time in coordinates A. Then, the observer in the coordinates A considers the length of B1C2 as the length of line segment of rectangle B1B2B3B4
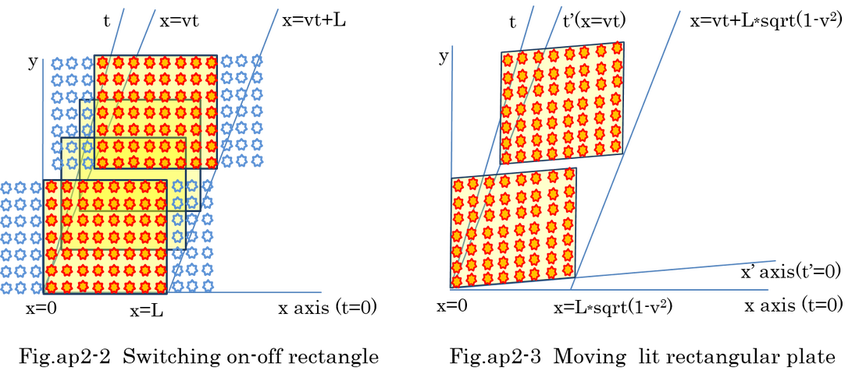
Fig.ap2-2 and Fig.ap2-3 indicate two types of moving rectangle. The first is the lattice of countless LED lamps. 56(7*8)LED lamps light up at the same time. When 7 lamps in the right side are switched on, 7 lamps are switched off in the left side. These lamps are shifting one after another. All of the lamps are fixed in coordinates A. No matter how fast these 56 lamps are shifting, there will not be Lorentz contraction in the coordinates A. The second is a moving plate of 56 LED lamps. There is a typical Lorentz contraction because the plate is moving with the velocity v in coordinates A. Although these two rectangles are moving, physical phenomena are different.
<Appendix 3 --- Time dilation>
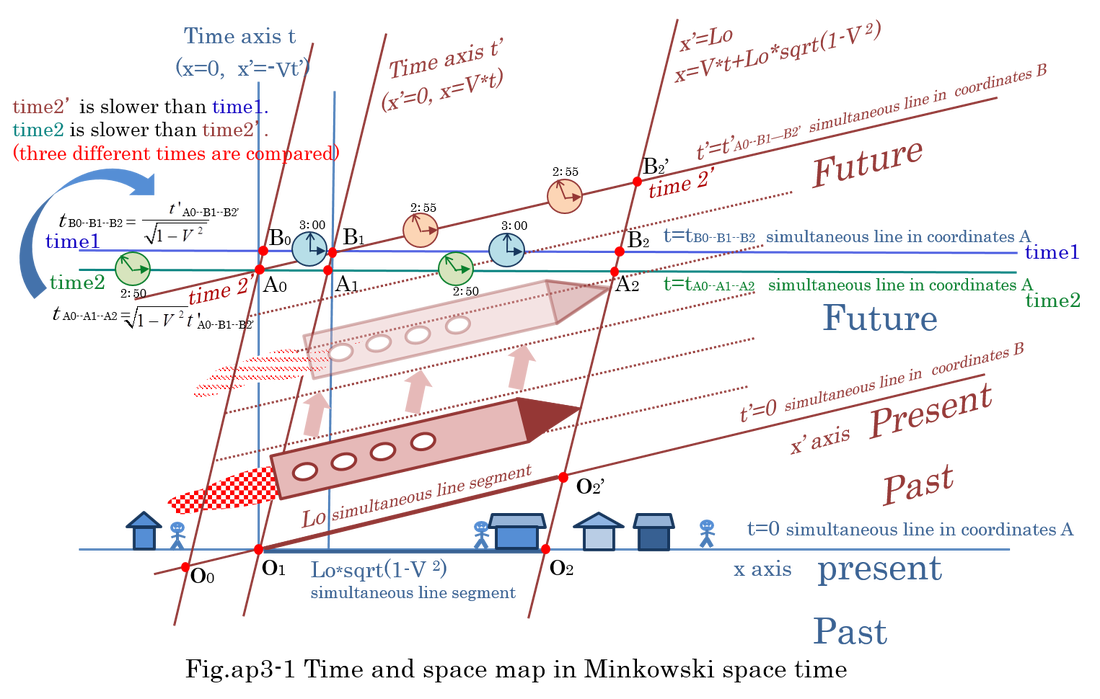
Time dilation is well known as well as Lorentz contraction. Fig.ap3-1 shows the reason why two watches in different coordinates slow each other. Rocket is moving with velocity V in the coordinates A. Coordinates B is also moving with velocity V. When the rocket reaches B1, the time in coordinates A is t Bo--B1--B2 which is simultaneous world in coordinates A. B1 and A0 are also included in t' Ao--B1--B2' which is simultaneous world in coordinates B. Stationary observer in coordinates A considers t Bo--B1--B2 is longer than t Ao--B1--B2' because proper time is shortest. The rear point of rocket, B1 is moving with the velocity V in coordinates A. According to Lorentz transformation (see equation 5-1), t Bo--B1--B2 is equal to 1/sqrt(1-V^2)*t' Ao--B1--B2' .
On the contrary, moving observer in the rocket considers t' A0--B1--B2' is longer than tAo--A1--A2 similarly because proper time is shortest. The original point, A0 is moving with the velocity -V in coordinates B.
In short, inequality is shown as t Bo--B1--B2 > t' Ao--B1--B2' > t Ao--A1--A2. The conclusion is that three different times (time1>time2'>time2) are compared at different places.
On the contrary, moving observer in the rocket considers t' A0--B1--B2' is longer than tAo--A1--A2 similarly because proper time is shortest. The original point, A0 is moving with the velocity -V in coordinates B.
In short, inequality is shown as t Bo--B1--B2 > t' Ao--B1--B2' > t Ao--A1--A2. The conclusion is that three different times (time1>time2'>time2) are compared at different places.
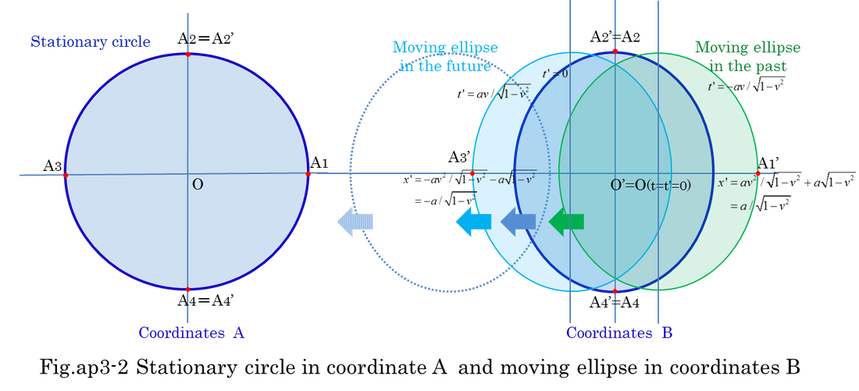
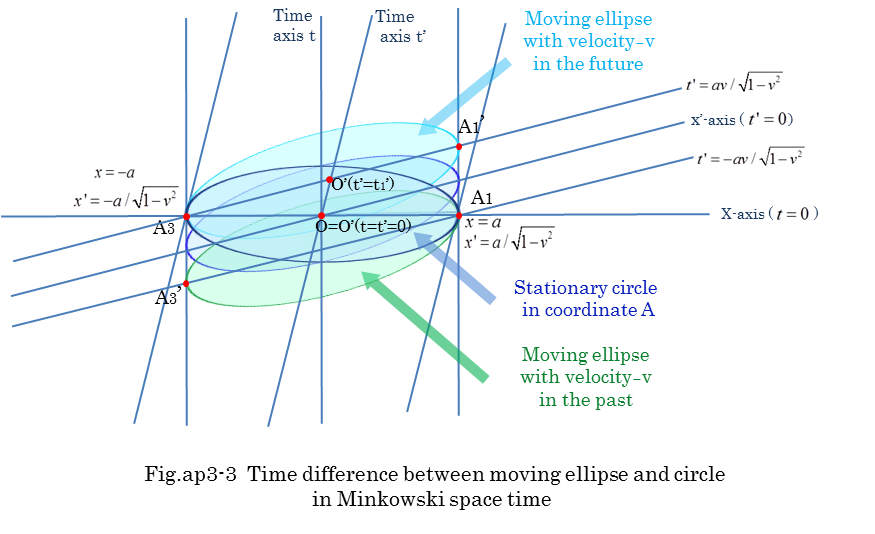
To get the intuition of contraction and time dilation, an example of stationary circle in coordinates A is shown in Fig-ap3-2. The circle is observed in moving coordinates B with velocity v. The radius(a) of the circle contracts into a*sqrt(1-v^2). A1 and A3 in coordinates A exist in different time in coordinates B. Surprisingly, A1 and A3 are included in different ellipses in the different time of coordinates B. Line segment A1'A3' is not a minor axis of a ellipse in coordinates B.
Fig.ap3-3 indicates the reason why A1' and A3' are in different ellipse in Minkowskiy space-time. Moreover, x'-coordinate of A1' is a/sqrt(1-v^2) and x'-coordinate of A3' is -a/sqrt(1-v^2). The length of minor axis is not 2a/sqrt(1-v^2) but 2a*sqrt(1-v^2).
The distance of O'A3 is not a*sqrt(1-v^2) but a/sqrt(1-v^2). O'(t'=t') is not the center of ellipse but the origin of coordinates B because the ellipse is moving to left with velocity -v in coordinates B.
The distance of O'A3 is not a*sqrt(1-v^2) but a/sqrt(1-v^2). O'(t'=t') is not the center of ellipse but the origin of coordinates B because the ellipse is moving to left with velocity -v in coordinates B.
Stationary circle is expressed by equation (ap3-1). According to Lorentz transformation, its shape changes to ellipse in coordinates B. Time and x-coordinates of A1 and A3 are calculated in equation (ap3-4,ap3-5,ap3-6,ap3-7)
<Appendix 4 --- Spherical light wave>
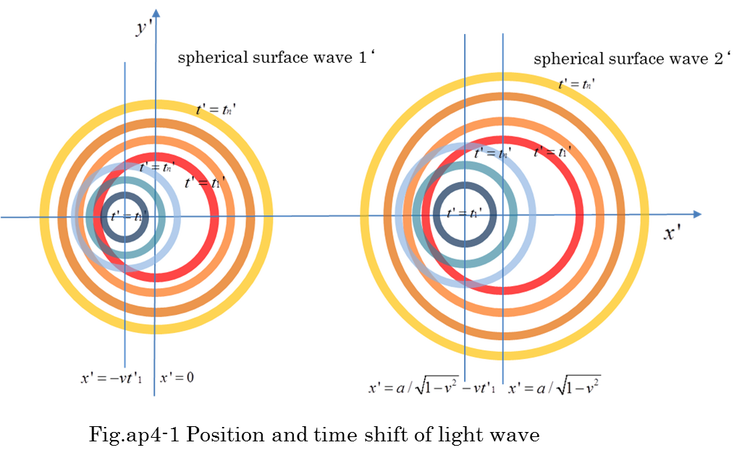
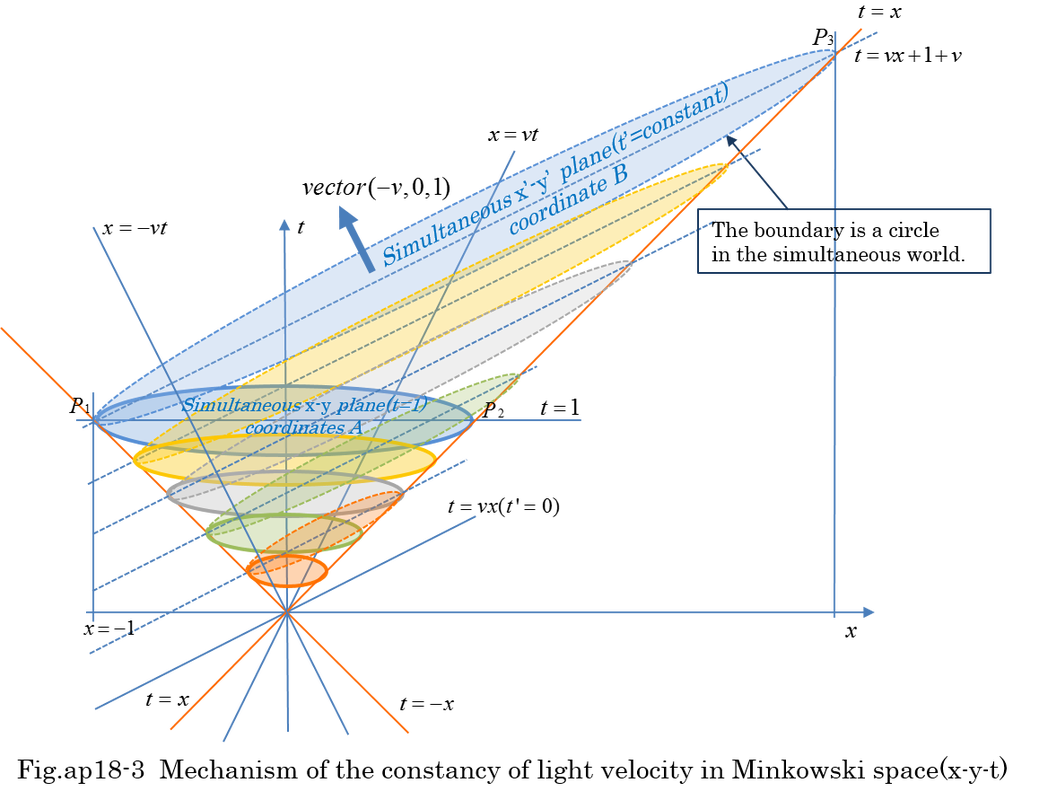
Supposed that light is spreading from the star in coordinates A. Star-1 is shining at the origin of Coordinates A. Coordinates B is moving along x axis of coordinates A with velocity v. Time is adjusted t=t'=0 when both origins of coordinates A and coordinates B coincides. The top of light surface of the spherical wave is expressed by equation (ap4-1). According to Lorentz transformation, equation (ap4-2) is obtained. Using equation (ap4-2), the surface of the spherical wave is similarly expressed by equation (ap4-3). This means the velocity of light is the same in both coordinates. Lorentz transformation is originally based on this equation.
Furthermore, we consider the light of star-2 is spreading from the position (x=a, y=0,z=0) in the coordinates A as shown in equation (ap4-4). How will the top of light surface of the spherical wave be seen in coordinates B ?
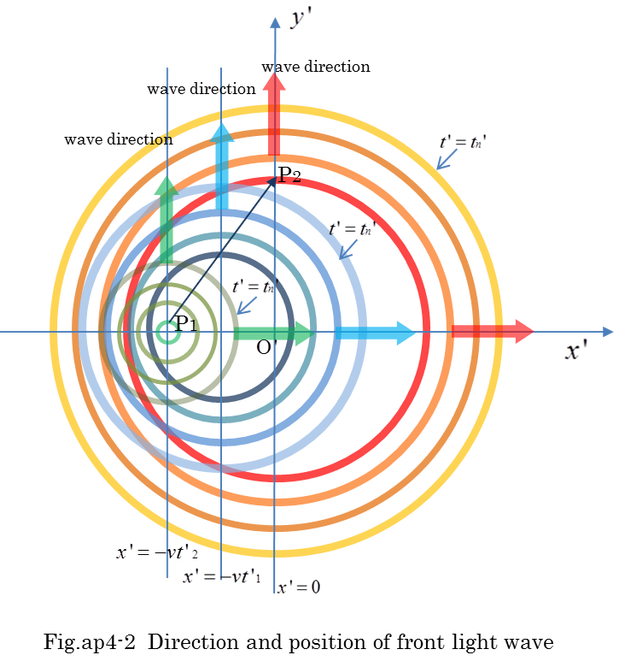
By substituting equation (ap4-2) into equation (ap4-4), equation (ap4-5) is obtained. Using x^2-t^2=x'^2-t'^2, equation (ap4-7) is finally obtained. The position of center of spherical wave is shifted from a to a/sqrt(1-v^2). The time of spreading is also shifted by a*v/sqrt(1-v^2). Fig.ap4-1 and Fig.ap4-2 show the position and time shift in coordinates B.
However, this phenomenon has no relation to well-known aberration in the field of astronomy. In case of so called aberration, Telescope's elevation angle shift is sin(p)=v/c. Angle p is the difference from right angle.
Comparing equation (ap4-1) and (ap4-3), it is wonder that the center of spherical light wave is the same in both coordinates. When the spherical light wave is spreading, the center of light wave is the origin of coordinate B. However, we expect the light wave continues being generated one after another at the origin of coordinates A. Subsequent waves are not expected to be concentric in coordinates B. According to relativistic velocity composition, when light velocity u=1 or -1 in coordinates A which moves in coordinates B with velocity -v, the synthetic velocity of light is always 1 or -1 because the velocity of one side is (1-v)/(1-1*v)=1 and the velocity of opposite side is (-1-v)/(1+1*v)=-1. That would make it no wonder that the center of the first light wave which was emitted at t=t'=0 never changes while it spreads. The Radius of other wave which is emitted at t=t1 is smaller than the first wave. When the observer watches waves in the coordinates B, all the light waves are not concentric circle. By tracing the light wave which was generated for an infinitesimal time, we can imagine the concentric circle. On the other hand, all the light waves are concentric in coordinates A.
However, this phenomenon has no relation to well-known aberration in the field of astronomy. In case of so called aberration, Telescope's elevation angle shift is sin(p)=v/c. Angle p is the difference from right angle.
Comparing equation (ap4-1) and (ap4-3), it is wonder that the center of spherical light wave is the same in both coordinates. When the spherical light wave is spreading, the center of light wave is the origin of coordinate B. However, we expect the light wave continues being generated one after another at the origin of coordinates A. Subsequent waves are not expected to be concentric in coordinates B. According to relativistic velocity composition, when light velocity u=1 or -1 in coordinates A which moves in coordinates B with velocity -v, the synthetic velocity of light is always 1 or -1 because the velocity of one side is (1-v)/(1-1*v)=1 and the velocity of opposite side is (-1-v)/(1+1*v)=-1. That would make it no wonder that the center of the first light wave which was emitted at t=t'=0 never changes while it spreads. The Radius of other wave which is emitted at t=t1 is smaller than the first wave. When the observer watches waves in the coordinates B, all the light waves are not concentric circle. By tracing the light wave which was generated for an infinitesimal time, we can imagine the concentric circle. On the other hand, all the light waves are concentric in coordinates A.
Equation (ap4-7) indicates that the position of circle's center is x'=a/sqrt(1-v^2) in coordinates B. Someone may think that the length of a is the distance in coordinates A, therefore, a should contract to a*sqrt(1-v^2) in coordinate B. However, we must remember that the position (x=a,t=0) and (x=0,t=0) do not exist in the simultaneous space-time in coordinate B. The position of star-2 from the origin of coordinates B can be calculated from four conditions { x=(x'+vt')/sqrt(1-v^2), t=(t'+vx')/sqrt(1-v^2), t=0, x=a }. The result of calculation is x'=a'=a/sqrt(1-v^2). When four conditions (t=0, x=a, t'=not 0, x'=a') are substituted into Lorentz transformation, the time of the origin in coordinates B is t'=-a*v/sqrt(1-v^2). On the other hand, we must remember Lorentz transformation means that time adjusting is done under the conditions (t=0,t'=0,x=0,x'=0).
The next step is consideration of continuous light waves. The top of the surface of spherical light wave which is generated t=t1 in coordinates A is expressed by equation (ap4-8).
This spherical light wave can be observed in coordinates B. It is expressed by equation (ap4-12). The light waves generated at the origin of coordinates A is shifted by -vt1' because coordinates B is moving. Someone may doubt t1'=t1/sqrt(1-v^2) in equation (ap4-12) is longer than t1. Referring to Minkowski space-time, the uncertain point will be cleared. The event(x=0,t=t1 light generation) is on the simultaneous line (t'=t1' constant time line slopes up).
Fig.ap4-2 indicates the direction and the position of light wave in coordinates B. Because the source of light is moving in coordinates B, the subsequent light wave which is close to light source exists close to the point (x'=-vt', y'=0) in coordinate B. The observer in coordinates B feels that it looks like light beam goes forward diagonally from P1 to P2. If actual light passed from P1 to P2, the velocity of light would be sqrt(1+v^2). It is impossible to exceed 1. Apparent light pass ( from P1 to P2 ) is made of a lot of front light waves. Refer to Fig.ap18-2 in appendix 18.
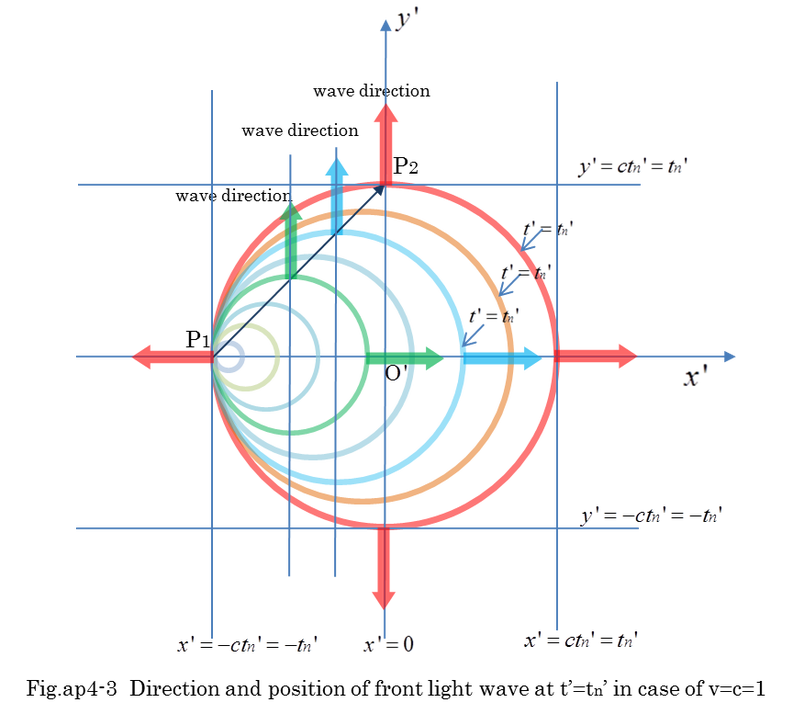
Fig.ap4-3 indicates the direction and position of light wave in the simultaneous space-time in case of v=c=1. When the coordinates B is moving with the velocity v which is almost close to 1, the top of front wave of left side always coincides with the light source.
Above analysis is the surface of sphere. Electromagnetic field of spherical wave is well known
(wikipedia.org/wiki/Wave_equation 7). Equation (ap4-13) and (ap4-14) are spherically symmetric.
(wikipedia.org/wiki/Wave_equation 7). Equation (ap4-13) and (ap4-14) are spherically symmetric.
Partial differential equation of wave function E(t,x,y,z) is also expressed by variables of (t',x',y',z'). Equation (ap4-15) indicates that any wave function satisfies the same form of differential equation in coordinates B.
Following is the calculation procedure of Partial differential equation.
<Appendix 5 --- Accelerated motion in special relativity >
What is accelerated motion in special relativity? Uniform accelerated motion is impossible to continue permanently in a certain inertial coordinates because v(velocity) must be less than 1(light velocity). However, there are two possible accelerated motions. The one is following motion A. A moving object can be accelerated by constant force. The other is virtually uniform accelerated motion B.
At first, Motion A is considered. Four vector's equation (ap5-1,ap5-2) indicates the accelerated motion in special relativity. Observer in the moving object is also accelerated by pseudo-constant four vector force.
At first, Motion A is considered. Four vector's equation (ap5-1,ap5-2) indicates the accelerated motion in special relativity. Observer in the moving object is also accelerated by pseudo-constant four vector force.
Velocity is calculated from equation (ap5-1,ap5-2,ap5-3). The relation between the velocity in inertial reference frame and proper time in the accelerated object is expressed by equation (ap5-4). The velocity of object never exceeds the light speed (v=1) even if proper time is infinite.
The distance from original point(x=0) in the reference coordinates is expressed by equation (ap5-7).
To examine the relation between x and t, it must be calculated by solving differential equation (ap5-8). Equation (ap5-8) is converted to differential equation of rational function as equation (ap5-11).
By introducing a complicated variable(T), differential equation (ap5-13) is obtained. x is indirectly expressed by two equations (ap5-14,15).
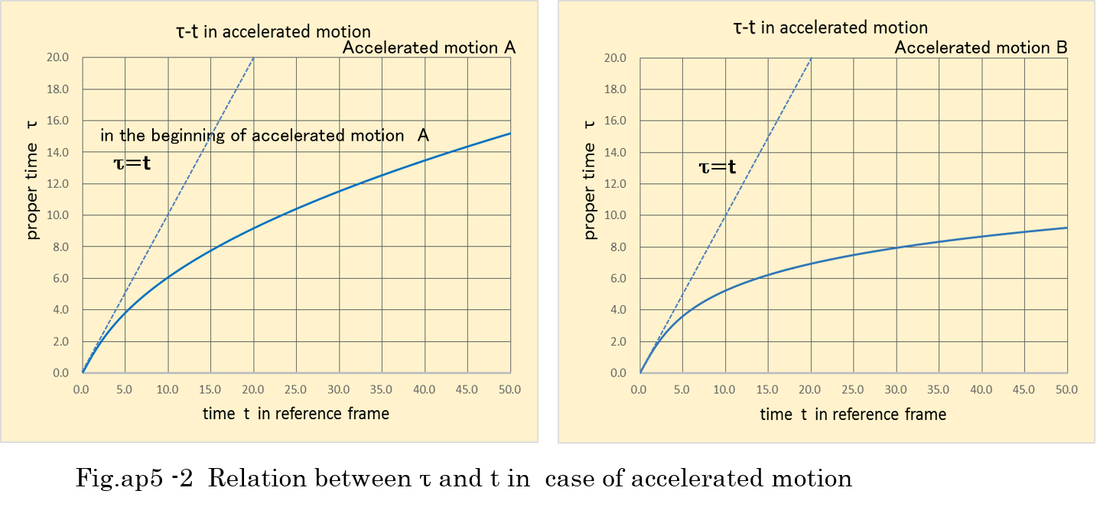
After elapse of infinite time, velocity is almost light speed. The elapse of time in reference coordinates is a quadratic function of proper time as shown in Fig.ap5-2. Observer in the moving object still considers that the motion is continually accelerated.
Next is motion B. In case of motion B, the velocity of a object is successively accelerated in moving inertial coordinates. The increase of velocity is constant in successive inertial coordinates whose velocity always coincides with the velocity of the object.
Equation (ap5-21) is Lorentz transformation between moving inertial coordinates(x',τ) and initial coordinates(x,t). dτ is infinitesimal proper time in moving inertial coordinates. dx'/dτ is expressed by equation (ap5-22). Increase of dx'/dτ is expressed by equation (ap5-23) because dx/dt=v when dτ is zero. Uniform acceleration is expressed by equation (ap5-24).
Equation (ap5-21) is Lorentz transformation between moving inertial coordinates(x',τ) and initial coordinates(x,t). dτ is infinitesimal proper time in moving inertial coordinates. dx'/dτ is expressed by equation (ap5-22). Increase of dx'/dτ is expressed by equation (ap5-23) because dx/dt=v when dτ is zero. Uniform acceleration is expressed by equation (ap5-24).
Equation (ap5-24) is easily integrated. Relation between t (time in reference frame) and τ(proper time) is expressed by equation (ap5-29). τ is nearly equal to t in the beginning of accelerated motion as well as in case of motion A.
t (time in reference frame) and x (distance from original point) are expressed by hyperbolic function of τ(proper time). In the beginning of accelerated motion, x increases as quadratic function of t. x is finally close to t and v is nearly 1 (light speed).
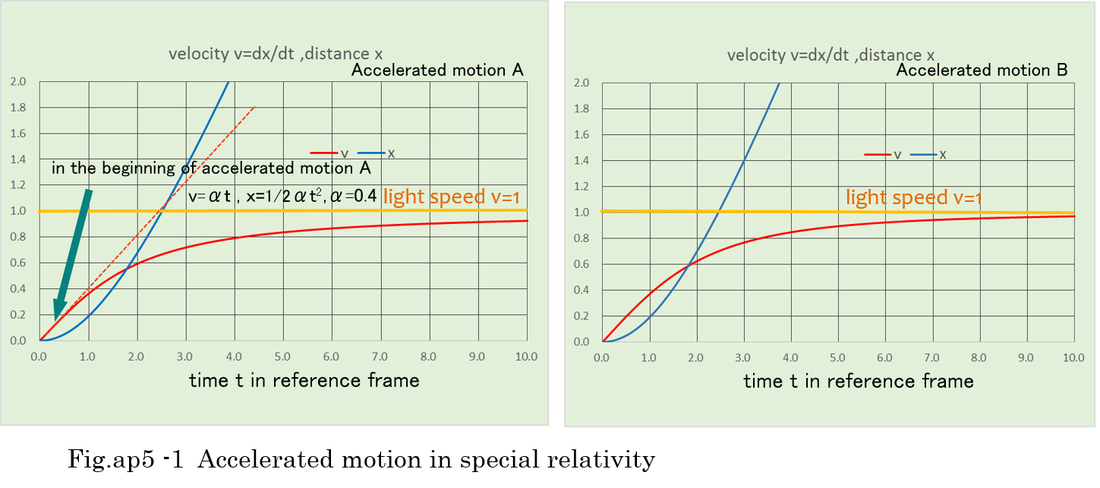
Fig.ap5-1 indicates velocity and distance in accelerated motion. It shows that dx/dt is gradually not accelerated and approaches to light speed. Acceleration of motion A is slower than motion B. Fig.ap5-2 indicates τ(proper time) is much slower than t(time in reference coordinates).
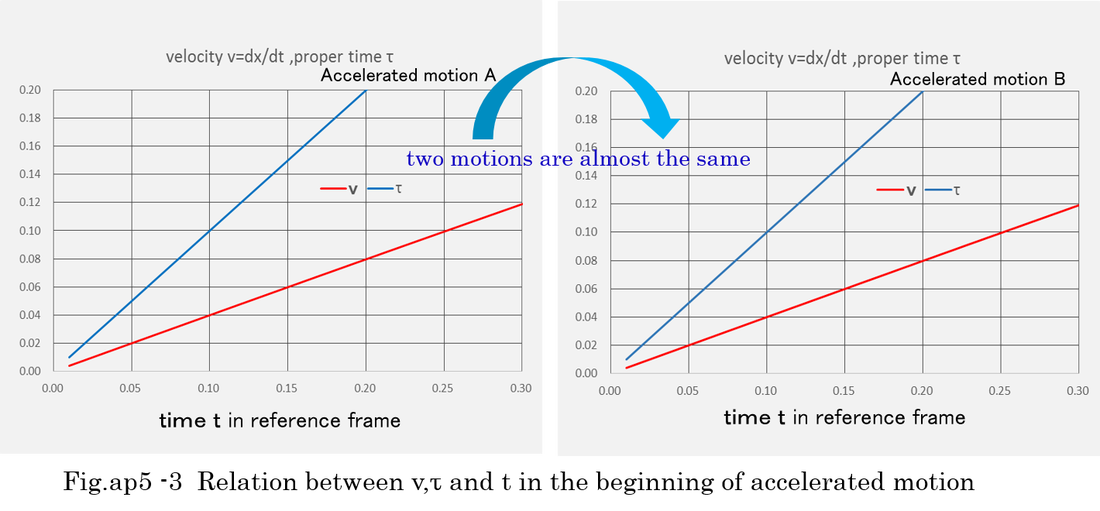
Equations (ap5-20), equation (ap5-30) and Fig.ap5-3 indicate t is nearly equal to τ because sqrt(1-v^2) is nearly equal to 1.
Equations (ap5-20), equation (ap5-30) and Fig.ap5-3 indicate t is nearly equal to τ because sqrt(1-v^2) is nearly equal to 1.
Comparing motion A with motion B, the length of four vector ( f4 ) is constant in motion B. Equation (ap5-36) indicates Motion B is really accelerated by constant four vector force.
Equation (ap5-37) indicates that acceleration vector in motion B can be transformed by Lorentz transformation. Invariant is the same as equation (ap5-36)
<Appendix 6 --- Variation of relativistic energy observed from different inertial frames>
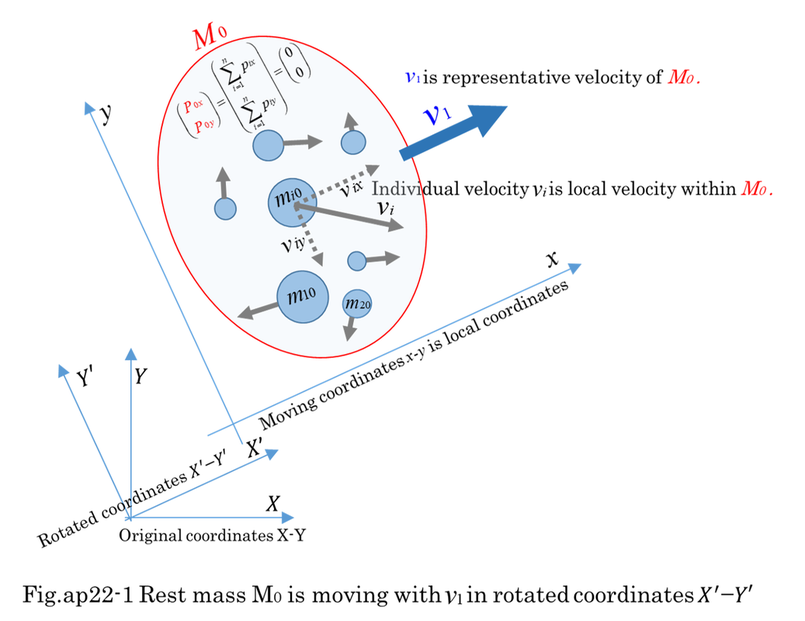
Relativistic mass(M) of a certain object consists of a lot of relativistic mass. It can be supposed that a lot of mass are moving with velocity (v1, v2, ....vi, ... , vn ) in a certain inertial coordinates. As it is explained in page 3, total energy (M) is the summation of mi/sqrt(1-vi^2), and total momentum(P=MV) is the summation of mivi/sqrt(1-vi^2). When the object being composed of a lot of relativistic mass is observed from different inertial coordinates, both M' and individual velocity(vi') vary according to the velocity(V') of inertial coordinates. M' is relativistic mass observed from different coordinates as shown in equation (ap6-1).
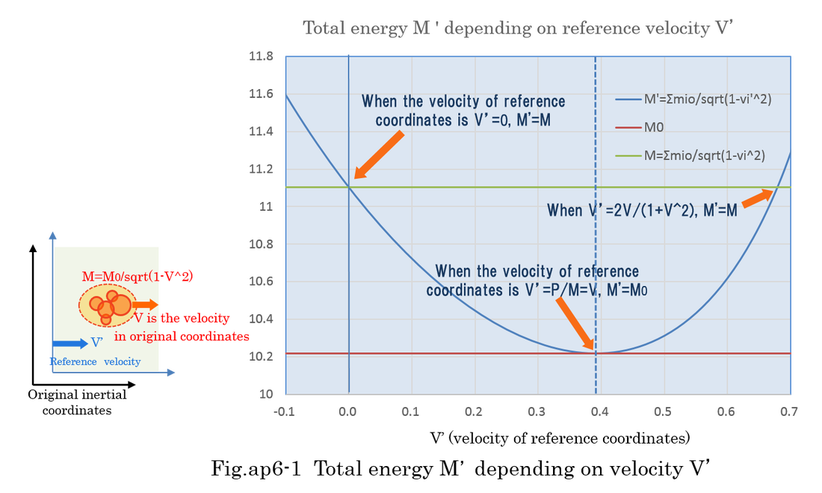
To calculate the variation of M', it needs to be partially differentiated with respect to V'. The result of differentiation is expressed by equation (ap6-6). The least value of M' is truly rest mass(M0) when the velocity(V') coincides with V(=P/M). Fig.ap6-1 indicates total energy(M') varies from infinite via M0 to infinite while V' changes from -1 to 1. Needless to say, M is equal to M0/sqrt(1-V^2) and M' is equal to M0 when V' is V(= P/M). It should be clear that Fig.ap6-1 does not show the variation of M but the one of M'. In addition, there are two points of intersection where M'=M. The one is V'=0, the other is V'=2V/(1+V^2). For example, when a car is runing at the speed of 100km/h, the observer who is runing at the speed of nearly 200km/h will see the car running at the speed of -100km/h.
<Appendix 7 --- Introduction of relativistic mass's formula>
How is a famous formula for relativistic mass introduced? There are several ways for introduction of the formula. It can be proved by using a famous formula for velocity composition in special relativity. As it is explained in page 3, equation (ap7-1) is an identical equation. Equation (ap7-2), (ap7-3) lead to the relation between u,v and composition velocity v'. Thus,v and v' can be considered as the velocity of a physical object. u is considered to be coordinates B's velocity in coordinates A. v is object's velocity in coordinates B. v' is object's velocity in coordinates A. Equation (ap7-4) is a pair of two equations which makes a four-vector. It can be rewritten as a matrix equation (ap7-5). This equation is applied for introduction of relativistic mass.
Equation (ap7-4), (ap7-5) are directly connected to mass and momentum by multiplication. If a object is moving with velocity v in coordinates B and coordinates B is moving with velocity u in coordinates A, a object is moving with the velocity v'=(u+v)/(1-uv). When the velocity of mass v=0 in coordinates B, mass is stationary. This means m=m0 in coordinates B. However, mass is moving in coordinate A. Therefore, using equation (ap7-7) or equation (ap7-8), equation (ap7-9) indicates that (m0,0) is transformed into (m',p'). From this result, the expression of m' =m0/sqrt(1-u^2) seems to be a moving mass when v' =u.
If m' is truly a moving mass, p'=m0v'/sqrt(1-v'^2) must be a momentum. There seems to be no objection concerning this explanation because mass m' must be moving with velocity of coordinates B when mass(m) is stationary in coordinates B.
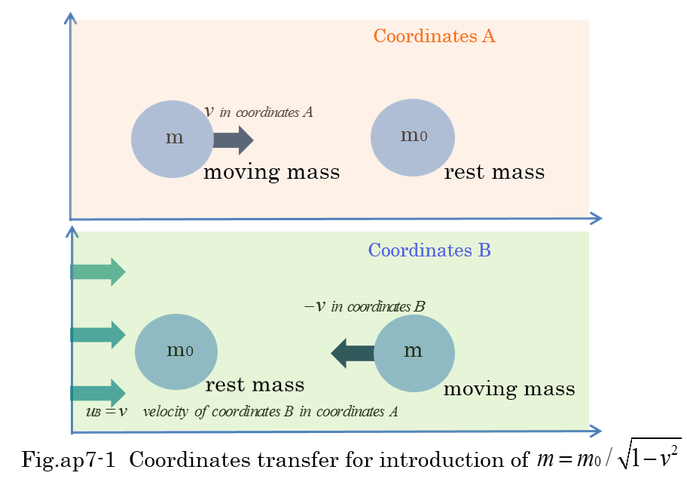
Furthermore, the concept that variable m=m0/sqrt(1-v^2) is moving mass can be proved under the situation as shown by Fig.ap7-1. The one mass is moving with velocity(v) and the other mass is stationary in coordinates A. Coordinates B is moving with the same velocity(uB=v) of moving mass. Moving mass and stationary mass are completely exchanged in coordinates B. Even if the formula m=m0/sqrt(1-v^2) is not known, it is required that (m',p') is the same value as (m,p) because both situations are symmetrical. Lorentz matrix equation (ap7-5),(ap7-6) are coincidentally derived from the synthesis of velocity and the definition of momentum(p=mv). Therefore, equation (ap7-10) is exactly the requirement for symmetric situation. Equation (ap7-11) is calculation of the right side term of equation (ap7-10). Equation (ap7-12) indicates that m is required to be m0/sqrt(1-v^2).
Furthermore, the concept that variable m=m0/sqrt(1-v^2) is moving mass can be proved under the situation as shown by Fig.ap7-1. The one mass is moving with velocity(v) and the other mass is stationary in coordinates A. Coordinates B is moving with the same velocity(uB=v) of moving mass. Moving mass and stationary mass are completely exchanged in coordinates B. Even if the formula m=m0/sqrt(1-v^2) is not known, it is required that (m',p') is the same value as (m,p) because both situations are symmetrical. Lorentz matrix equation (ap7-5),(ap7-6) are coincidentally derived from the synthesis of velocity and the definition of momentum(p=mv). Therefore, equation (ap7-10) is exactly the requirement for symmetric situation. Equation (ap7-11) is calculation of the right side term of equation (ap7-10). Equation (ap7-12) indicates that m is required to be m0/sqrt(1-v^2).
<Appendix 8 --- The difficulty of concept of rest energy in Newtonian mechanics>
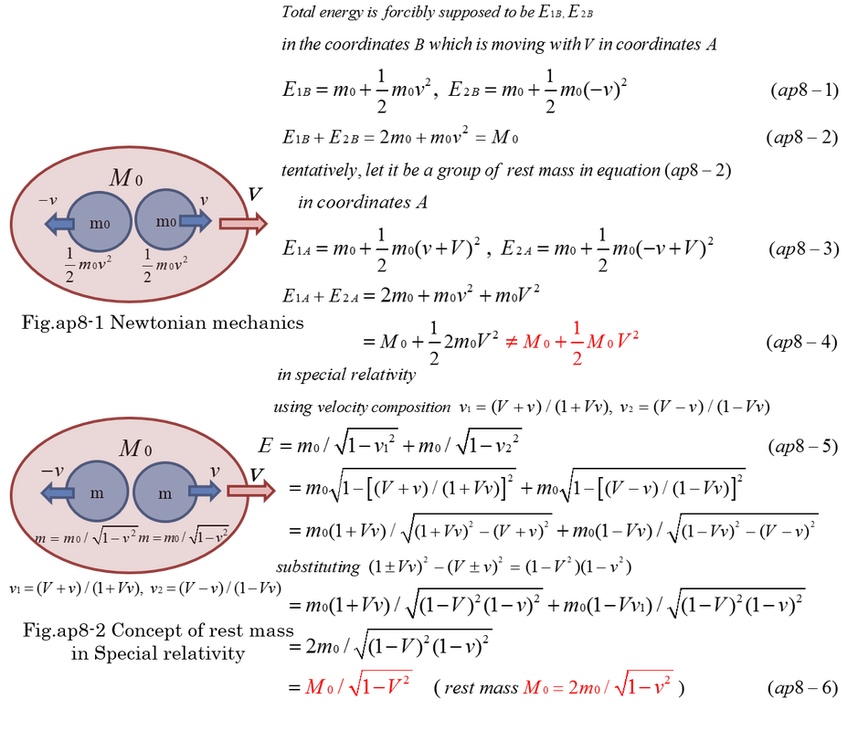
The concept of rest energy is not possible in Newtonian mechanics. Equation (ap8-1,2) is forcibly considered to be total energy. Although a rest mass is considered in Fig.2-4 in the previous chapter2, equation (ap8-3,4) indicates the total energy of a pair of masses can not be expressed in the same format. In special relativity, M0 can be considered to be a rest mass of a pair of masses as shown in equation (ap8-5,6) because it is expressed in the same format. Of course, its momentum is zero.
<Appendix 9 --- Exponential summation of zero rest mass>
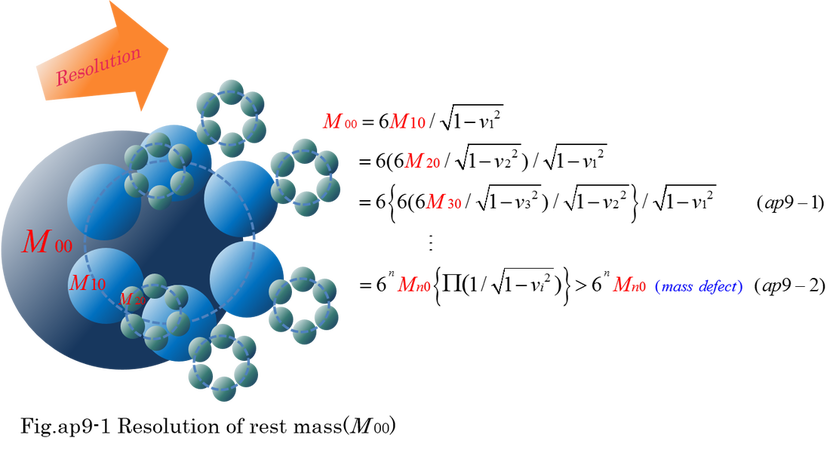
The object is usually made of countless molecules and atoms. An example of simplified resolution model is shown by Fig.ap9-1. M0 is redefined as M00. Rest mass(M00) is divided by 6 moving particles. Divided particle is repeatedly divided by 6 moving particles. The first subscript(i) represents times of resolution. The second subscript (0) represents rest mass. For example, M30 means a rest mass which is resolved three times from M00 into 6^3 pieces. At each resolution step(i), rest mass is Mi0(i=0,1,2 --- n). Equation (ap9-1,2) indicates M00 is expressed by multi-products of 6/sqrt(1-vi^2) and Mn0. Mn0 is the smallest rest mass after n times procedure of dividing mass. Total of rest mass is 6^n*Mn0, but it is not equal to M00 at all. M00 contains internal kinetic energy. When n approaches infinite value, Mn0 approaches the infinitesimal. Therefore, everyone expects that 6^n*Mn0 approaches the finite value such as M00. Surprisingly, even if n approaches infinite value, 6^n*Mn approaches zero as shown by equation (ap9-4). In general, even if division parameter, integer(k) is larger than 6, equation (ap9-6) is satisfied. Equation (ap9-6) indicates that Mn0 is unequal to M00/6^n unless there is no internal kinetic energy. The condition that all of vi=0 is unrealistic.
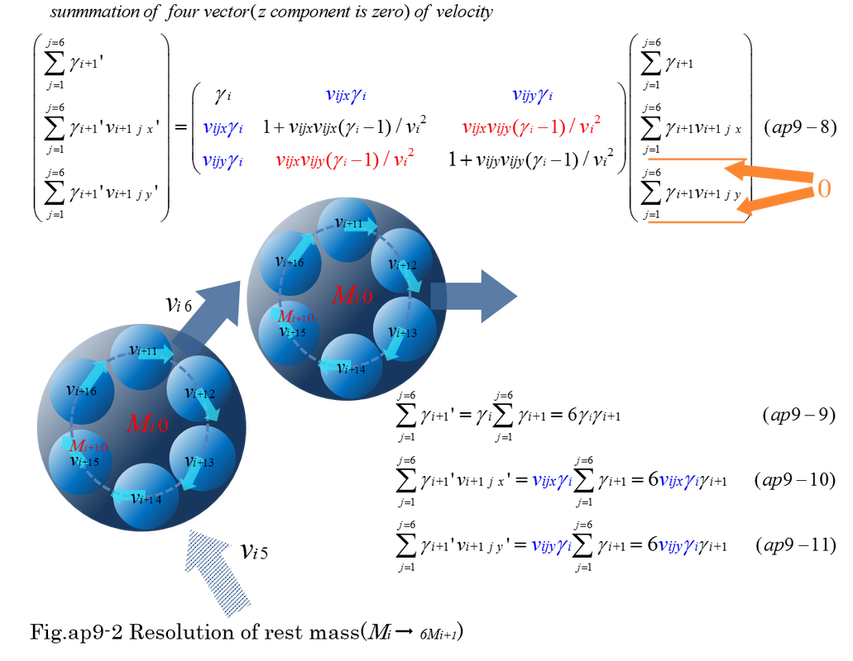
Lorentz transformation of four-vector leads to the concept of resolution of rest mass M00. In order to make the procedures clear, equation (ap9-7) is expressed for transformation from local velocity vi+1 j to local velocity vi+1 j'. vi+1 j' is the velocity which is observed from the center of Mi0. We must remember Mi0 is also moving with the velocity vi j.
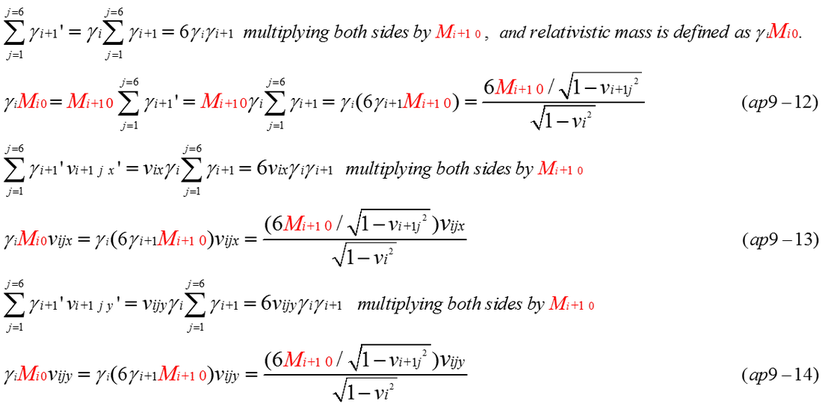
There are six rest mass(Mi+1) going around, which is the component of Mi. From four-vector, relative mass and momentum is obtained. By summing equation (ap9-7), equation (ap9-8) is obtained. In the right side of summation of four-vector is zero except for the first component. Results of matrix calculation is equation (ap9-9,10,11).
From Lorentz transformation of velocity, the relation of resolution of rest mass Mi0 and Mi+1 0 is obtained. By combining six moving rest masses, rest mass(Mi 0) has zero momentum in it's local coordinates. The procedure of resolution of rest mass in x-y-t space time is satisfied as well as in equation (6-11,12) in t-x space-time.
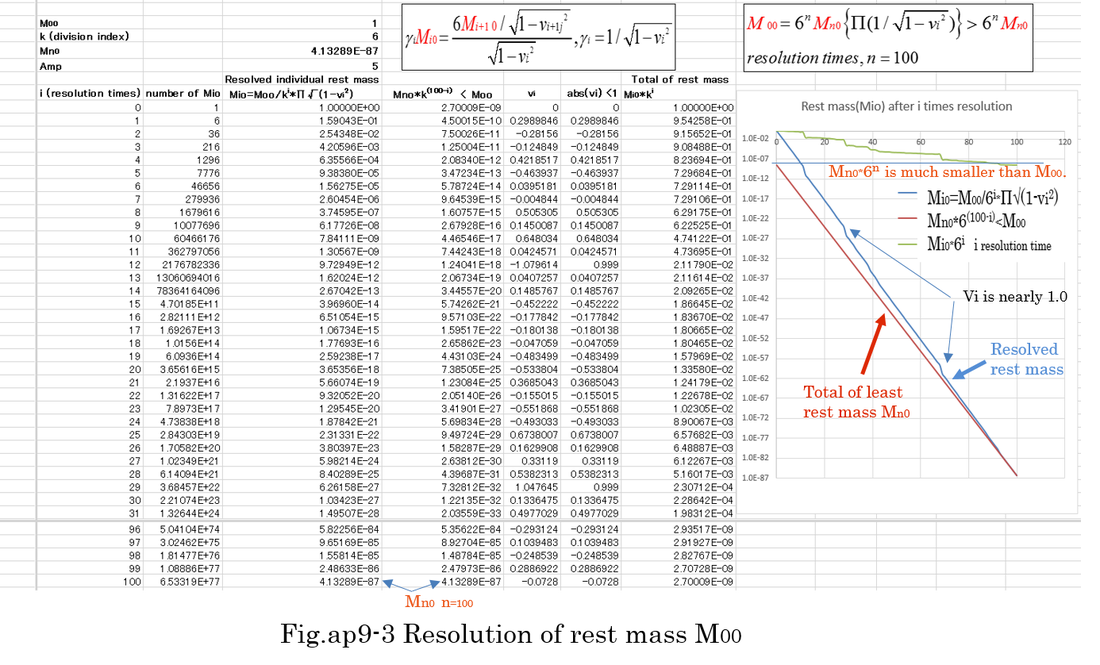
Fig.ap9-3 is an example of resolution of mass(M00). Division index k is 6. Each velocity(vi) is generated by random number by one step of resolution. When vi happens to exceed 1(light velocity), vi is forced to be 0.999 in order to continue calculation. Maximum time(n) of resolution is 100. mn0 is the smallest rest mass. Calculation result indicates the total of rest mass(mn0*6^100) is much smaller than M00.
If resolution continues infinitely, not only Mn0, but also Mn0*6^100 will approach zero. In actual computer calculation, when the resolution continues infinitely, the result of calculation of mn0 is replaced with zero perfectly.
If resolution continues infinitely, not only Mn0, but also Mn0*6^100 will approach zero. In actual computer calculation, when the resolution continues infinitely, the result of calculation of mn0 is replaced with zero perfectly.
Equation (ap9-4,5) and Fig.ap9-3 imply that rest mass(M00) consists of kinetic energy and rest mass. Even if the summation of rest mass is close to zero, rest mass M00 is a finite value because of inner kinetic energy. Furthermore, there is a possibility that the attraction of gravity can be compared with the repulsion of electric charge when inner velocity is close to light velocity. Electric force is proportional to Ke*e^2/r^2, but gravitational force is proportional to G*m0^(2n)/π(1-vi^2)/r^2 although Ke is by far larger than G.
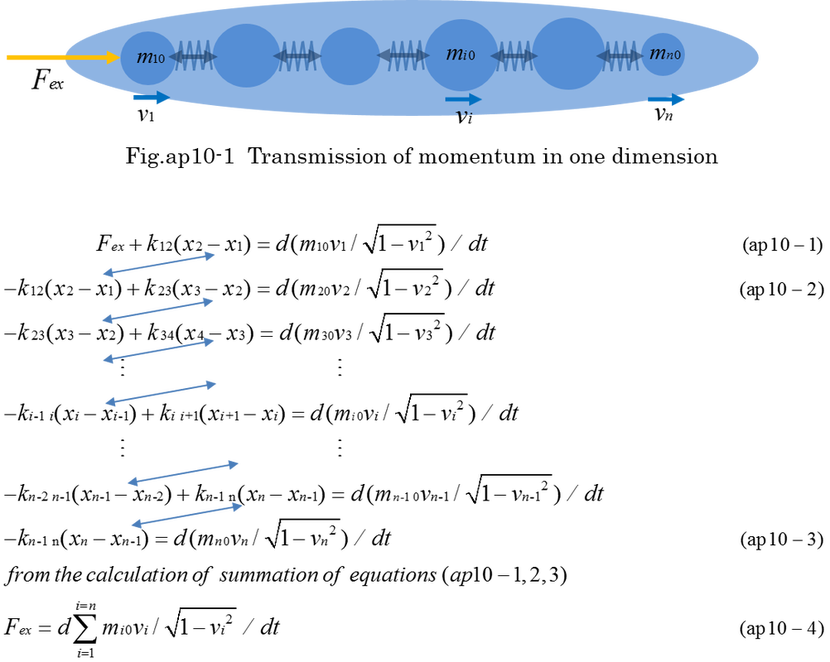
<Appendix 10 --- Transmission of momentum in one dimensional object>
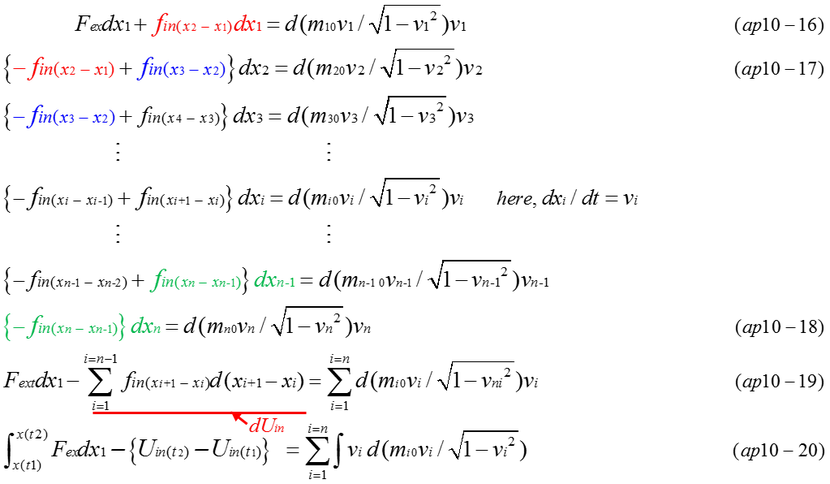
Fig.ap10-1 indicates that a lot of rest masses are connected by springs. Equation (ap10-1,2,3,4) indicates that internal forces are cancelled by springs. kij is spring constant. However, there remains a difficult question as to whether each restoring force is equal on both sides of spring. It is a difficult question that we have to put on hold. At this time , restoring force is supposed to be equal because spring is massless. This supposition may cause a calculation error when the velocity is close to light velocity.
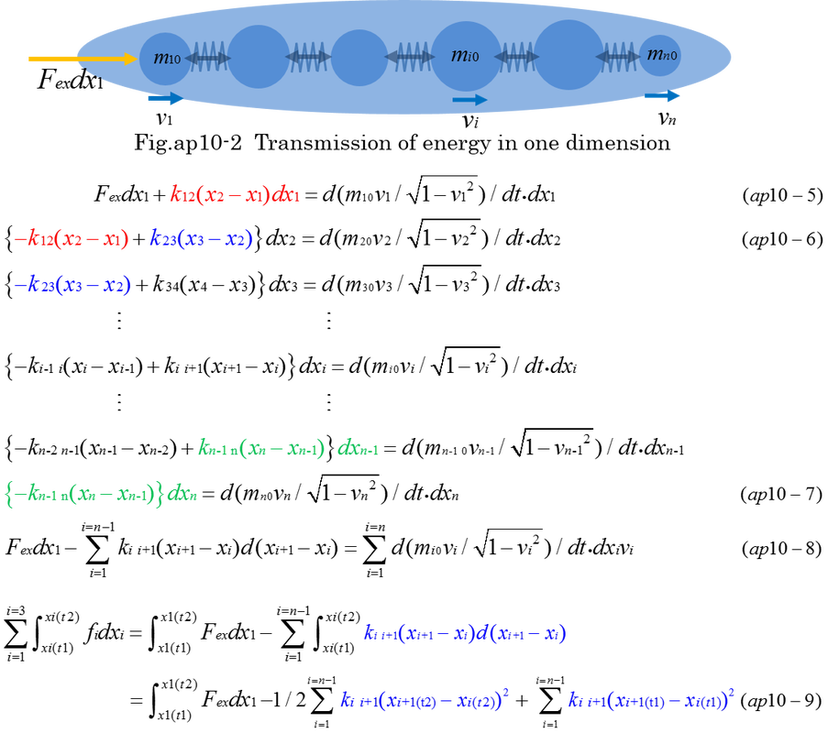
If kij(xj-xi) is by far larger than inertial force, Fex is nearly equal to -kij(xj-xi) and distance(xj-xi) is nearly zero when spring is strong. Furthermore, when inertial force is negligible and all of the spring constants are the same, the individual velocity is nearly equal each other because equation (ap10-1) is almost the same as equation (ap10-2,3). That means dxi/dt =dxj/dt and mi0 is strongly combined with neighboring rest masses. Then, M0=m10+m20+m30. There is no meaning of individual velocity(v1,v2,v3). However, individual rest mass(mi0) independently moves in some cases. M0 is considered to be not constant, but it can be defined in common as an invariant in all inertial frames.
If kij(xj-xi) is by far larger than inertial force, Fex is nearly equal to -kij(xj-xi) and distance(xj-xi) is nearly zero when spring is strong. Furthermore, when inertial force is negligible and all of the spring constants are the same, the individual velocity is nearly equal each other because equation (ap10-1) is almost the same as equation (ap10-2,3). That means dxi/dt =dxj/dt and mi0 is strongly combined with neighboring rest masses. Then, M0=m10+m20+m30. There is no meaning of individual velocity(v1,v2,v3). However, individual rest mass(mi0) independently moves in some cases. M0 is considered to be not constant, but it can be defined in common as an invariant in all inertial frames.
In general, internal force fi is different each other when independent inertial force of internal mass is not negligible. As it was formerly explained, M0 is a combined rest mass. Increase of kinetic energy must be calculated individually because M0(rest mass) is not constant. However, M0 can be calculated as an invariant in the instantaneous inertial frame.
Supposing that the affinity of molecules depends on distance and the collision is elastic, attraction is expressed by equation (ap10-11). The collision force is canceled by the law of action and reaction. The affinity is also canceled as it is expressed by equation (ap10-11,12). However, the affinity accumulates as bonding energy.
For example, a group of three rest masses is considered. m10,m20,m30 are moving with the velocity of v1,v2,v3 respectively. Relativistic mass(M) and momentum(P) are expressed by equations (ap10-20,21). V(=P/M) is a representative velocity of relativistic mass(M). v1,v2,v3 are local velocity.
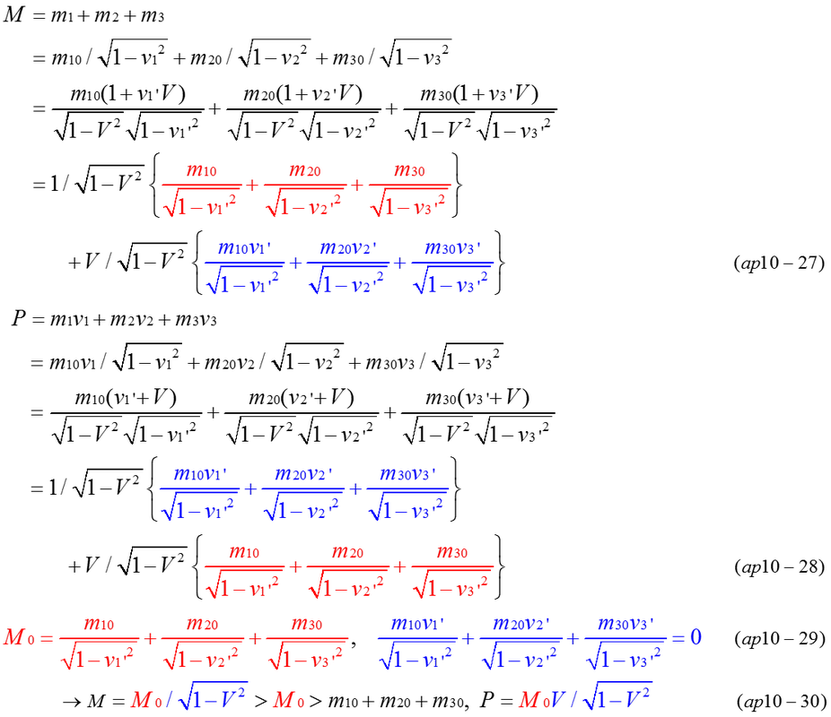
Red part of equation is rest mass(M0) and blue part is momentum of rest mass(M0). When V and M0 are decided, the momentum of M0 must be zero in equation (ap10-27).
There is always an inertial frame which makes the momentum of combined masses zero. Fig.ap10-3 indicates that zero momentum is created from a combination of arbitrary m1,m2,m3 and v1,v2,v3. Then, equation (ap10-29) and equation (ap10-30) are automatically satisfied when vi'=(vi-V)/(1-viV) and V=P/M.
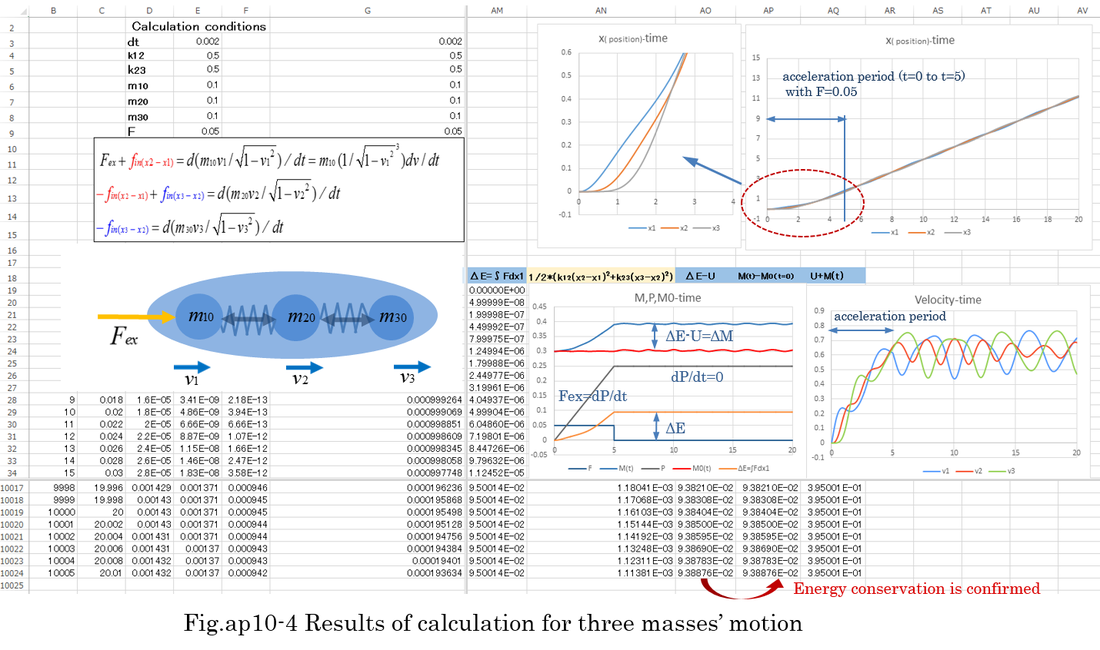
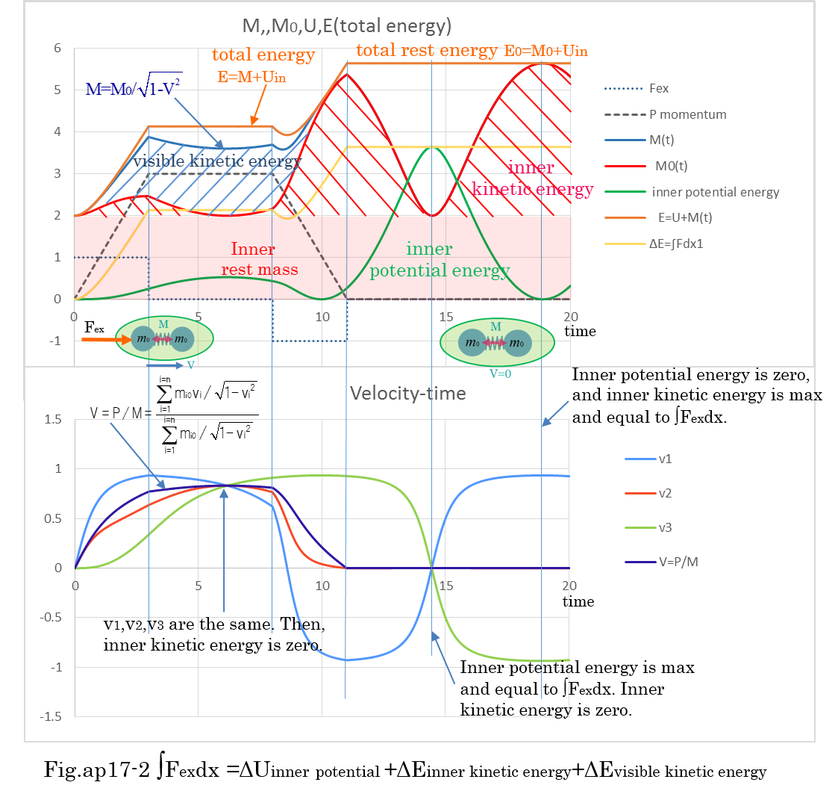
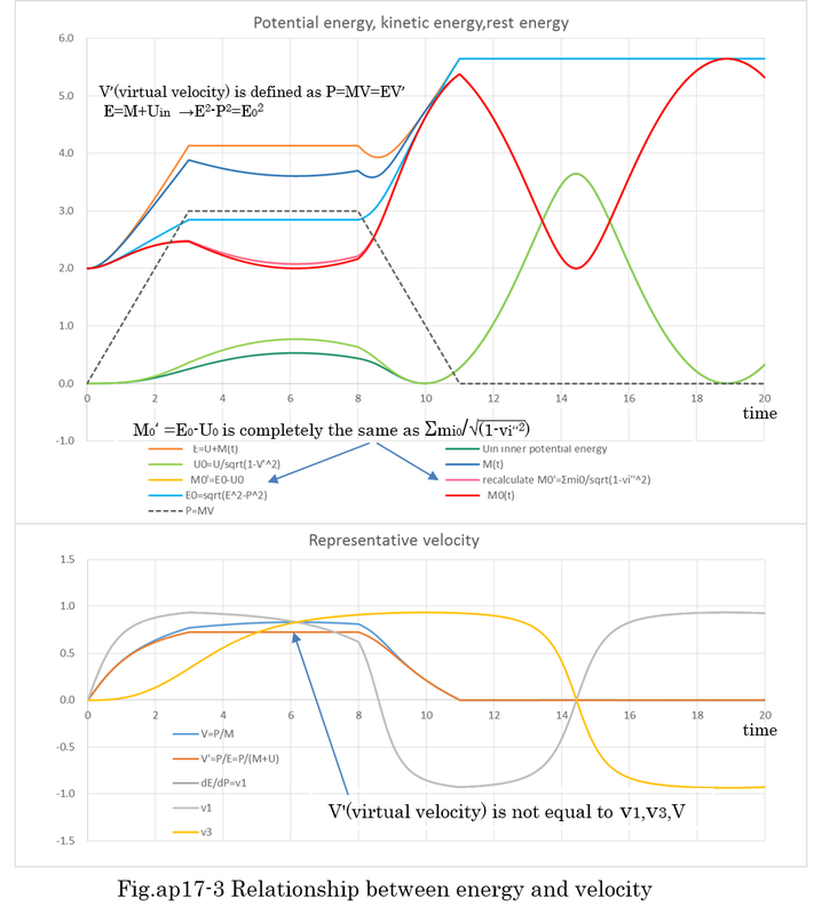
Equation (ap10-34) indicates the increase of energy(ΔE) is exactly the sum of ΔU+ΔM. Internal potential energy does not include relativistic mass(M) as long as kij is not identified. Although M0 can be decided as shown in equation (ap10-29), equation (ap10-35) indicates dM0/dt is not zero. That means M0 is not constant in general case. In case of separate motion of masses, the increase in energy of individual mass must be calculated as it is explained in equation (5-28) and equation(5-35). Based on equation (ap10-35), when dM0/dt is cyclical change, dv1,dv2,dv3 are cyclical. Rest mass has also cyclical value around the average of M0. After a short period momentum F0*Δt (F0 is constant) is applied, M and M0 are changing periodically as shown in Fig.ap10-4.
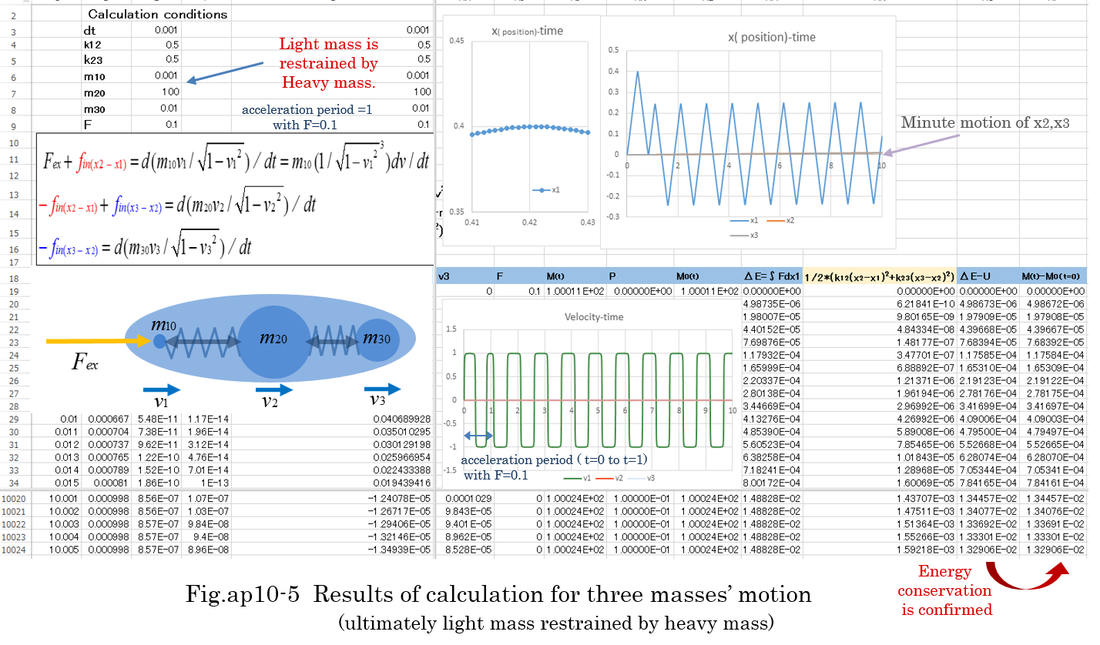
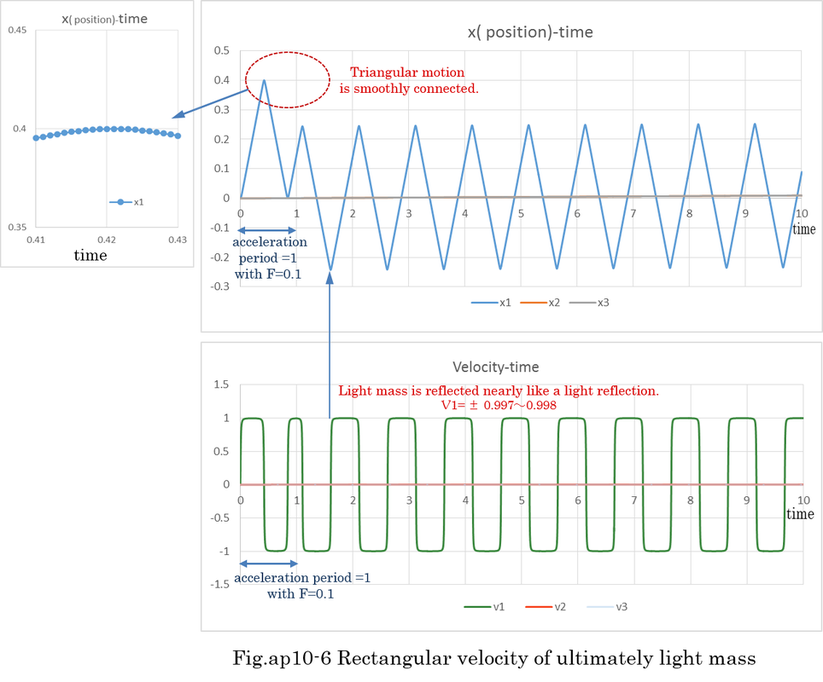
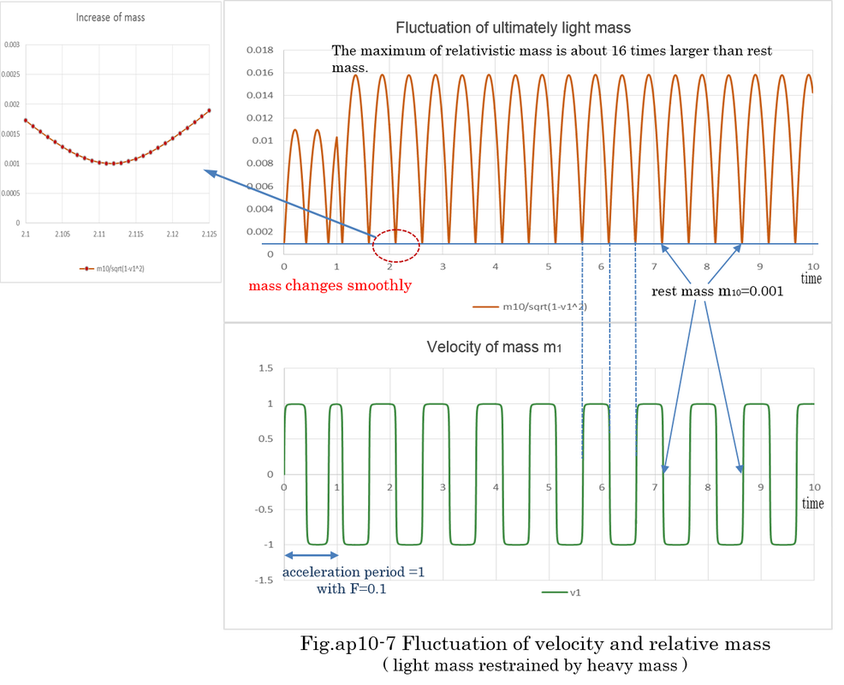
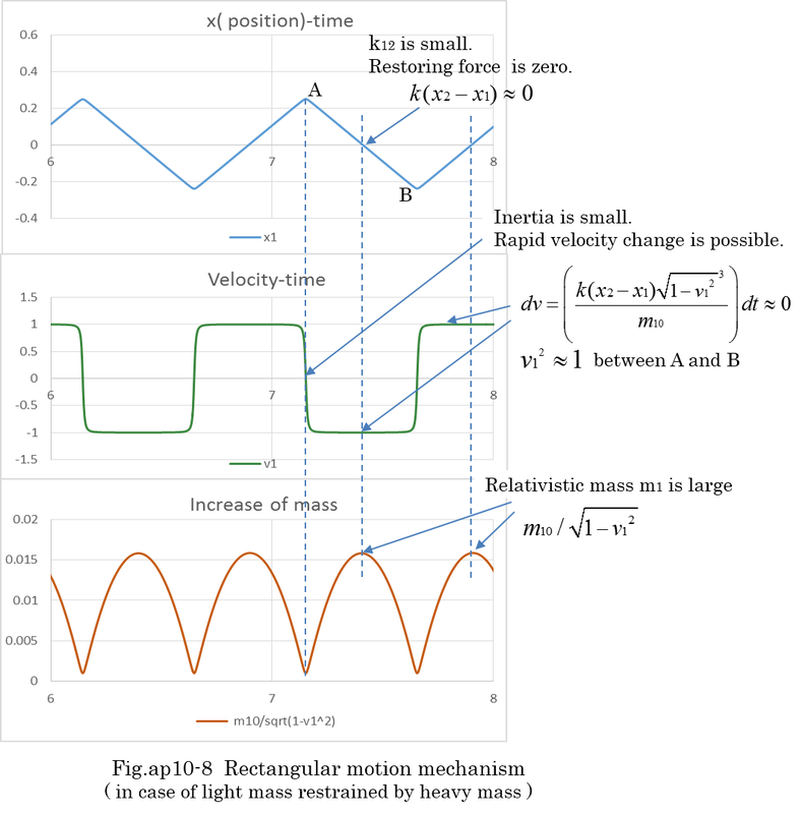
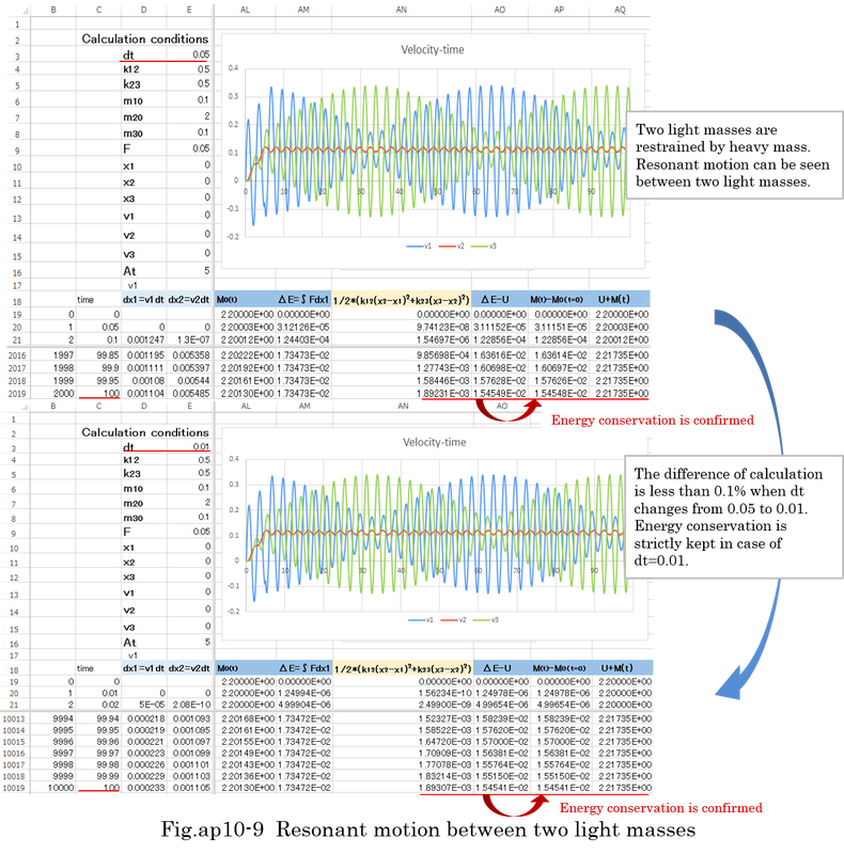
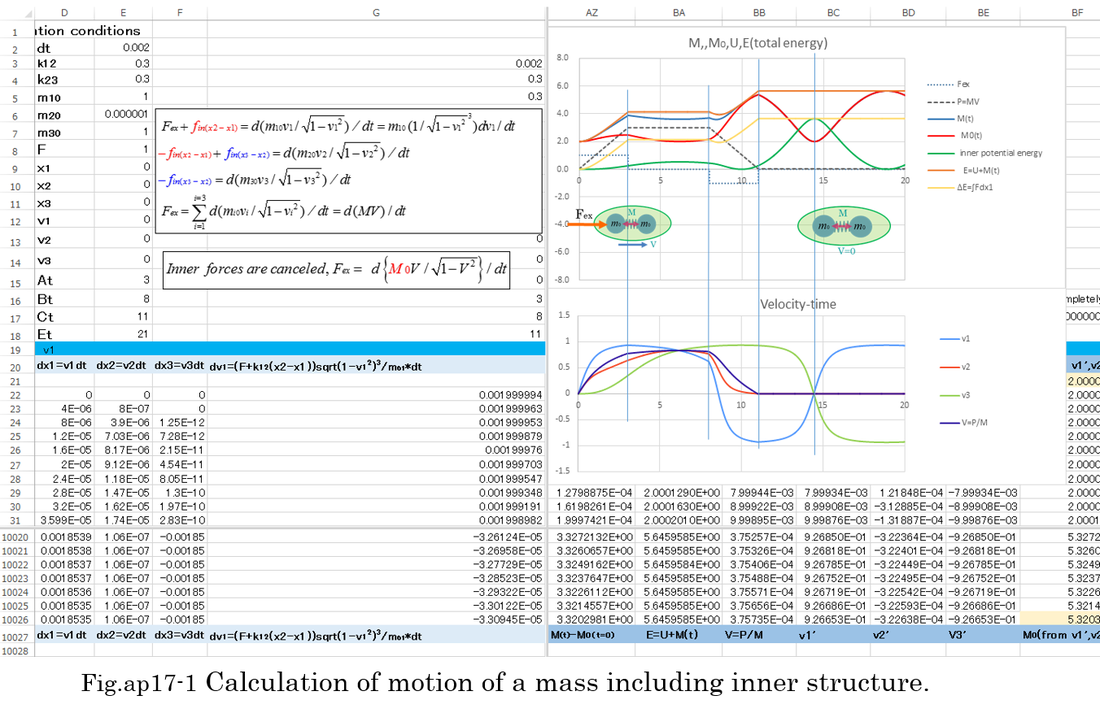
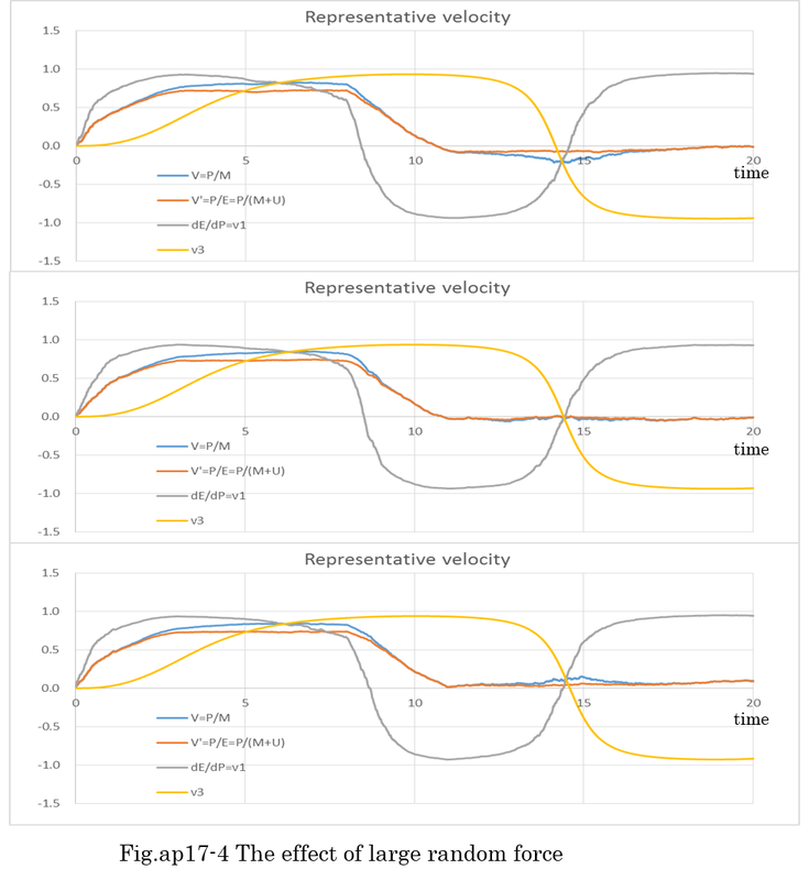
Examples of numerical calculation by Runge-Kutta method are shown Fig.ap10-4,5,6,7,8,9 . The Runge-Kutta method is able to calculate nonlinear differential equation. Fig.ap10-4 is the calculation of normal mass motion. Fig.ap10-5,6,7,8 is the calculation of ultimately light mass motion. Fig.ap10-9 is the calculation of resonant motion between two light masses which are restrained by heavy mass. In Fig.ap10-9, the accuracy of Runge-Kutta method is confirmed by changing dt(the length of time) from 0.01 to 0.05. The difference of two calculations is less than 0.1%. Further more, energy conservation indicates the accuracy of calculation. The results of calculation indicates equation (ap10-10) is theoretically right. In general, when the motion is cyclical, numerical calculation is expected to be stable (not divergent).
Runge-Kutta method
Differential equation must be written to simultaneous differential equation.
This time, unknown variables are x1,x2,x3,v1,v2,v3.
3 basic equations are following. d(mi0vi/sqrt(1-vi^2))/dt=kij(xj-xi)+Fexternal --- etc. ( refer to left side of Fig.ap10-4,5 )
Initial conditions are x1=x2=x3=0, v1=v2=v3=0, external force Fexternal=F(t=0) at time t=0.
Then, we can create 6 equations from 3 basic equations. It is necessary to create the type of dx/dt=func(**)
Three equations are very simple.
dx1=func1(x1,x2,x3,v1,v2,v3)*dt=v1dt ----(1)
dx2=func2(x1,x2,x3,v1,v2,v3)*dt=v2dt ----(2)
dx3=func3(x1,x2,x3,v1,v2,v3)*dt=v3dt ----(3)
4th,5th,6th equation are acceleration. (a little complicate)
dv1=func4(x1,x2,x3,v1,v2,v3)*dt=(F+k12(x2-x1))*sqrt(1-v1^2)^3/m10)*dt -------------(4)
dv2=func5(x1,x2,x3,v1,v2,v3)*dt=(-k12(x2-x1)+k23(x3-x2))*sqrt(1-v2^2)^3/m20)*dt ----(5)
dv3=func6(x1,x2,x3,v1,v2,v3)*dt=(-k23(x3-x2))*sqrt(1-v3^2)^3/m30)*dt ----------------(6)
These equations are solved directly. However, the accuracy of calculation is not enough.
Then, Runge-Kutta method is convenient and accurate.
Runge-Kutta method
Differential equation must be written to simultaneous differential equation.
This time, unknown variables are x1,x2,x3,v1,v2,v3.
3 basic equations are following. d(mi0vi/sqrt(1-vi^2))/dt=kij(xj-xi)+Fexternal --- etc. ( refer to left side of Fig.ap10-4,5 )
Initial conditions are x1=x2=x3=0, v1=v2=v3=0, external force Fexternal=F(t=0) at time t=0.
Then, we can create 6 equations from 3 basic equations. It is necessary to create the type of dx/dt=func(**)
Three equations are very simple.
dx1=func1(x1,x2,x3,v1,v2,v3)*dt=v1dt ----(1)
dx2=func2(x1,x2,x3,v1,v2,v3)*dt=v2dt ----(2)
dx3=func3(x1,x2,x3,v1,v2,v3)*dt=v3dt ----(3)
4th,5th,6th equation are acceleration. (a little complicate)
dv1=func4(x1,x2,x3,v1,v2,v3)*dt=(F+k12(x2-x1))*sqrt(1-v1^2)^3/m10)*dt -------------(4)
dv2=func5(x1,x2,x3,v1,v2,v3)*dt=(-k12(x2-x1)+k23(x3-x2))*sqrt(1-v2^2)^3/m20)*dt ----(5)
dv3=func6(x1,x2,x3,v1,v2,v3)*dt=(-k23(x3-x2))*sqrt(1-v3^2)^3/m30)*dt ----------------(6)
These equations are solved directly. However, the accuracy of calculation is not enough.
Then, Runge-Kutta method is convenient and accurate.
The 1st step is to obtain dx1,dx2,---,dv3 by using functions of (1),(2),---,(6).
Store these values as dx11,dx21,---,dv31.
The 2nd step is to obtain dx1,dx2,---,dv3 again by using functions of (1),(2),---,(6).
But, when calculating all of 6 functions, substitute x1+1/2*dx11 into x1, as well, x2+1/2*dx21 into x2,----- etc.
Store these values as dx12,dx22,---,dv32.
The 3rd step is to obtain dx1,dx2,---dv3 again by using functions of (1),(2),---,(6).
But, when calculating all of 6 functions, substitute x1+1/2*dx12 into x1, as well, x2+1/2*dx22 into x2,----- etc.
Store these values as dx13,dx23,---,dv33.
The 4th step is to obtain dx1,dx2,---,dv3 again by using functions of (1),(2),---,(6).
Substitution is a little different. When calculating of all functions , substitute x1+dx13 into x1, as well, x2+dx23 into x2,-----etc.
Store these values as dx14,dx24,---,dv34.
Finally, truly accurate dx1,dx2,dx3,dv1,dv2,dv3, are obtained from stored values.
dx1=1/6*(dx11+2*dx12+2*dx13+dx14)
dx2=1/6*(dx21+2*dx22+2*dx23+dx24)
dx3=1/6*(dx31+2*dx32+2*dx33+dx34)
dv1=1/6*(dv11+2*dv12+2*dv13+dv14)
dv2=1/6*(dv21+2*dv22+2*dv23+dv24)
dv3=1/6*(dv31+2*dv32+2*dv33+dv34)
Then, new values are x1+dx1, x2+dx2,---v3+dv3 and t+dt. Repeat these procedures. It is better that dt is small, but calculation will take long time. In case of the following calculations, dt is 0.001 or 0.002,10000steps using Excel 20l3.
---- Example 1. ----
Fig.ap10-5,6,7,8 indicates that ultimately light mass is reflected like light when heavy mass is 100,000 times larger than light mass. Regardless of the severe condition, energy conservation is confirmed through the Runge-Kutta method. The velocity of light mass changes like rectangular waves because of the nonlinear factor m10/sqrt(1-v^2)^3. Even if m10 is very small, the inertia of relative mass becomes enormous because the velocity of light mass(m10=0.001) approaches ±1. Once v1 is nearly ±1, it takes a considerable time to reduce the velocity because of the huge inertia.
----- Example 2. ----
----- Example 2. ----
If you need to check the calculation of example 2, click the following file.
| extream_motion_20140316.xlsx | |
| File Size: | 12103 kb |
| File Type: | xlsx |
---- Example 3. ----
---- Example 4. ----
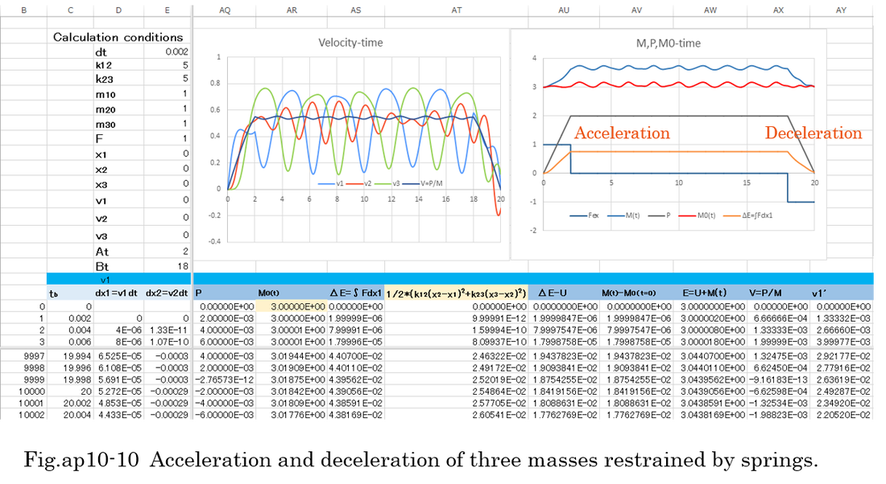
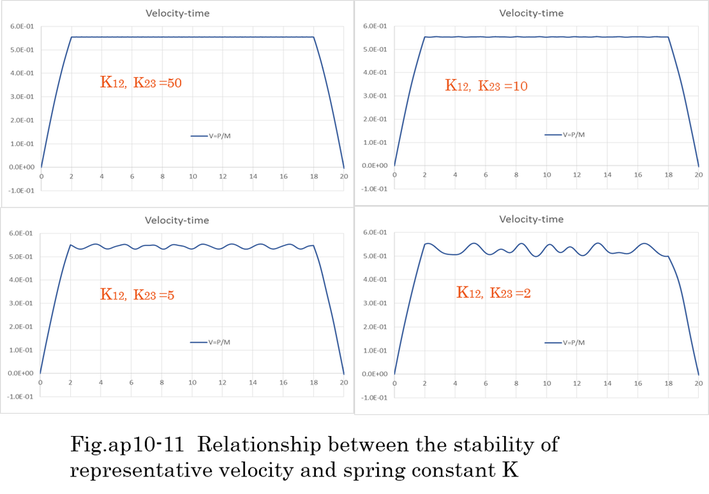
Three masses are restrained by springs. Left side mass is accelerated by external force for 2(sec). Upper right side of Fig.ap10-10 indicates that a group of three masses moves for 16(sec) without force, and is decelerated by external force for 2(sec). Each mass is fluctuated by springs. Representative velocity V(=P/M) is also fluctuated by the restoring force of springs. The fluctuation of representative velocity depends on spring constant k12 and k23 as shown in Fig.ap10-11. When masses are restrained by hard springs, the motion is close to rigid body's motion.
Three masses are restrained by springs. Left side mass is accelerated by external force for 2(sec). Upper right side of Fig.ap10-10 indicates that a group of three masses moves for 16(sec) without force, and is decelerated by external force for 2(sec). Each mass is fluctuated by springs. Representative velocity V(=P/M) is also fluctuated by the restoring force of springs. The fluctuation of representative velocity depends on spring constant k12 and k23 as shown in Fig.ap10-11. When masses are restrained by hard springs, the motion is close to rigid body's motion.
<Appendix 11 --- Four vector expression by Lorentz transformation in t-x-y dimension>
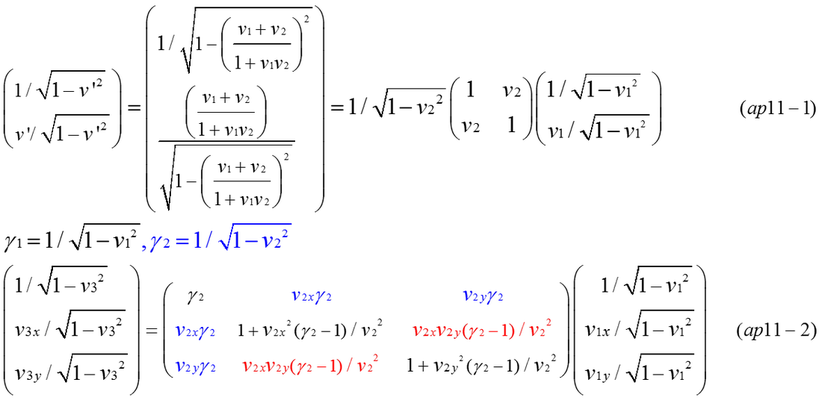
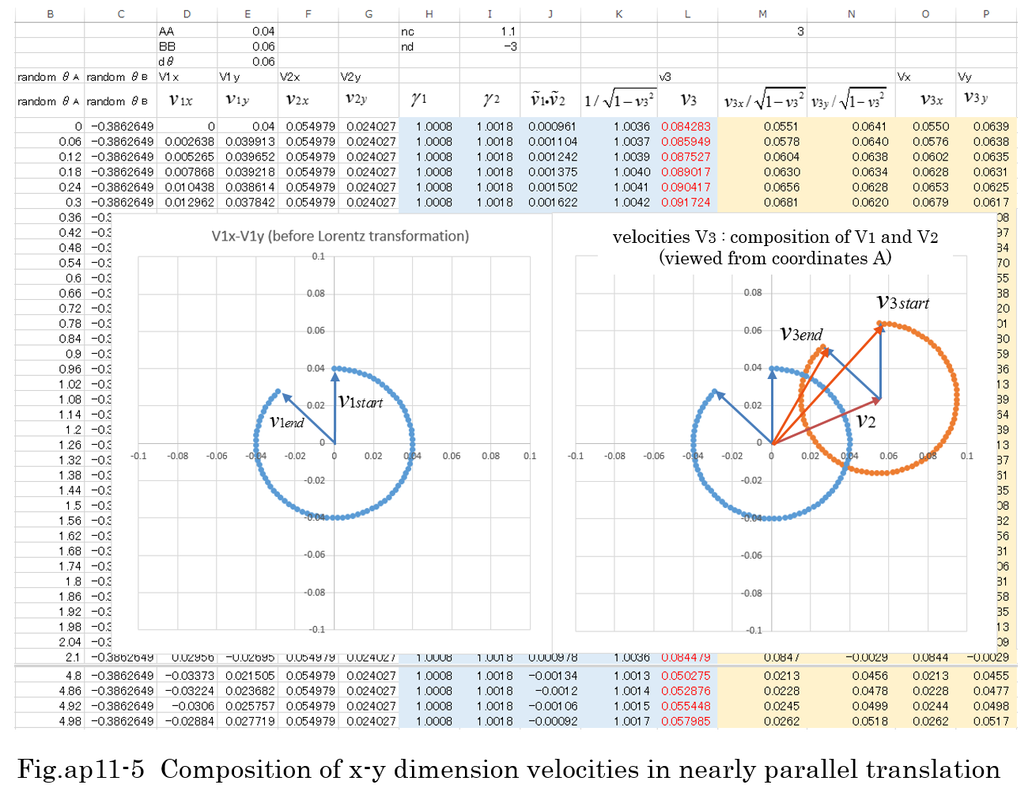
Equation (ap11-1) is an expression by Lorentz transformation of four vector velocity in t-x dimension. Four vector must be simply expressed by ( 1/sqrt(1-v^2),v/sqrt(1-v^2) ). In case of t-x dimension, it can be confirmed that transformed vector has the same formal expression of equation (ap11-1). It is difficult to show that complicated matrix calculations of four-vector can be expressed by the left side of equation (ap11-2). Equation (ap11-3,4,6,7,8,9) is results of complicated calculations. However, equation (ap11-4) is relatively simple. Although equations (ap11-5,8,9) are complicate, it can be confirmed that equation (ap11-4) is equal to equation (ap11-9) as long as numerical calculation is done. Fig.ap11-1 indicates v3 is the same value in some examples of calculation. The velocity composed of (v1,v2) is equal to v3=1 (light velocity) in the last row of calculations.
Composition of velocity v1 and v2 in t-x dimension is well known. A famous formula, v3=(v1+v2)/(1+v1*v2) is relatively simple. However, in case of t-x-y dimension, the synthesis of velocity is more complicate. The difference of direction of 2 vectors makes it difficult to calculate the composition of velocity.
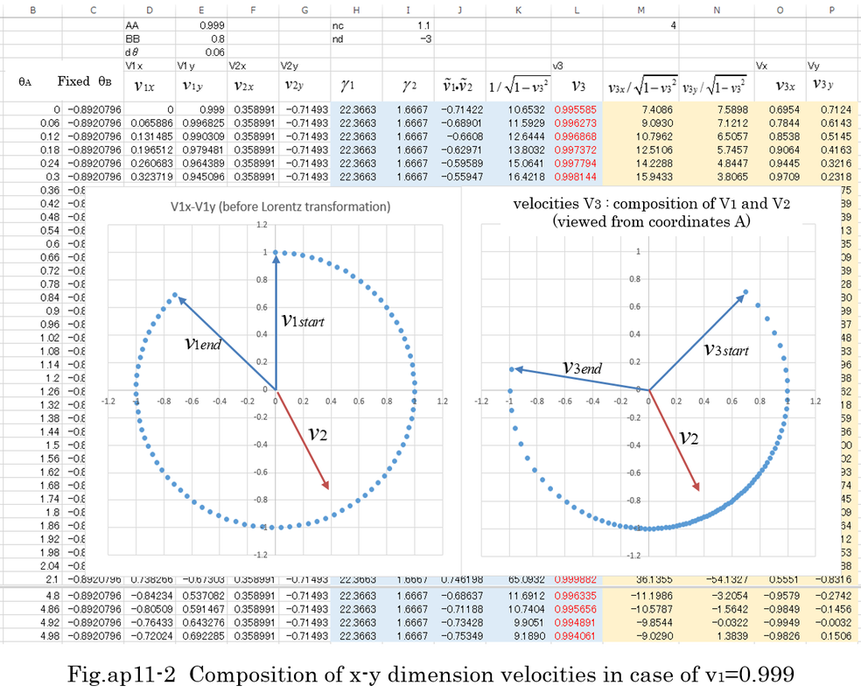
In Fig.ap11-2, changing the direction of velocity(v1) whose absolute value is 0.999( nearly light speed) in coordinates B, the velocity composition(v3) is calculated in coordinates A. The direction of velocity of coordinate B is supposed to be constant in coordinates A. The absolute value of velocity composition (v3) is naturally is nearly 1. The range of direction is smaller than that of v1.
In Fig.ap11-2, changing the direction of velocity(v1) whose absolute value is 0.999( nearly light speed) in coordinates B, the velocity composition(v3) is calculated in coordinates A. The direction of velocity of coordinate B is supposed to be constant in coordinates A. The absolute value of velocity composition (v3) is naturally is nearly 1. The range of direction is smaller than that of v1.
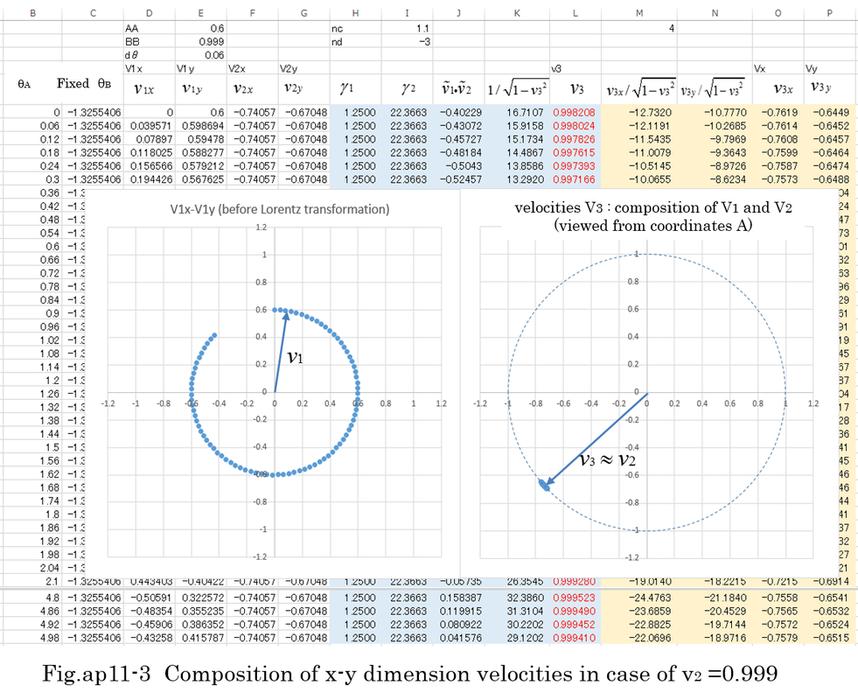
In Fig.ap11-3, changing the direction of velocity(v1) whose absolute value is 0.6 in coordinates B, the velocity composition(v3) is calculated in coordinates A. The direction of velocity(v2) of coordinate B is supposed to be constant and the absolute value of velocity is 0.999 in coordinates A. The composition of velocity,v3 is almost the same velocity(v2) regardless of the direction of v1.
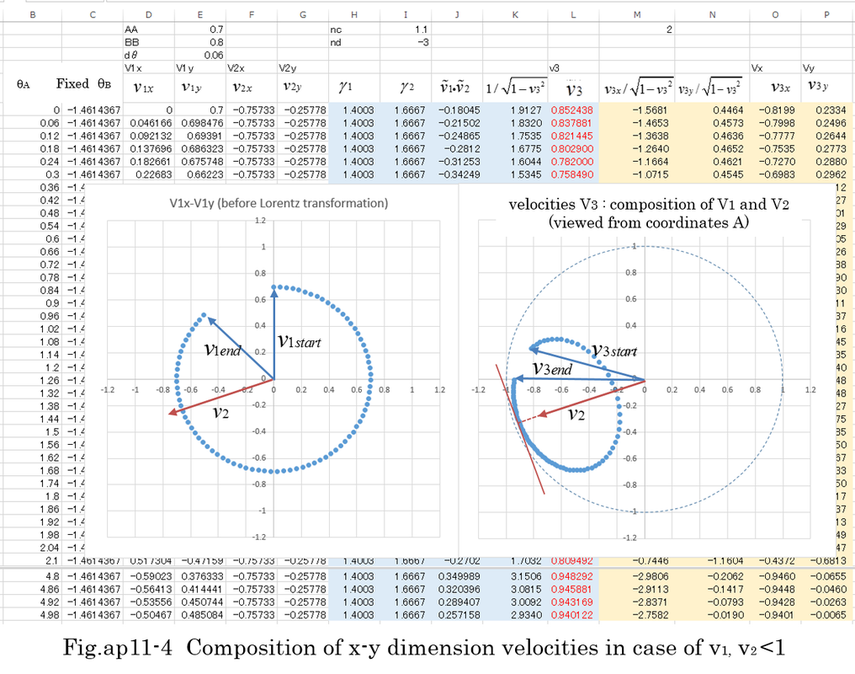
In Fig.ap11-4, changing the direction of velocity(v1) whose absolute value is 0.7 in coordinates B, the velocity composition(v3) is calculated in coordinates A. The direction of velocity(v2) of coordinate B is supposed to be constant and the absolute value of velocity is 0.8 in coordinates A. The range of velocity composition(v3) is narrower than that of velocity(v1). When v2 is close to 1, the range of v3 is getting narrow. In an extreme case, Fig.ap11-4 is getting similar to Fig.ap11-3. When the direction of v1 and v2 coincides, v3 has a maximum value of (v1+v2)/(1+v1*v2). The composition of v1 and v2 in t-x-y dimension also does not exceed light velocity as long as v1 and v2 do not exceed light speed.
In Fig.ap11-5, considering a small velocity whose absolute value is 0.04 in coordinates B, the velocity composition(v3) is close to parallel translation in coordinates A. The direction of velocity(v2) of coordinate B is supposed to be constant and the absolute value of velocity is 0.06 in coordinates A. 0.06 and 0.04 are much less than 1(light velocity). This example is close to normal vector calculation, (v3x,v3y)=(v1x+v2x,v1y+v2y).
If you need to check the calculation of 2 dimensional velocity , click the following file. You can input AA,BB whose values must be less than 1.
| 2dimension_velocity_20150225.xlsx | |
| File Size: | 151 kb |
| File Type: | xlsx |
<Appendix 12 --- Lorentz contraction of distance between moving objects>
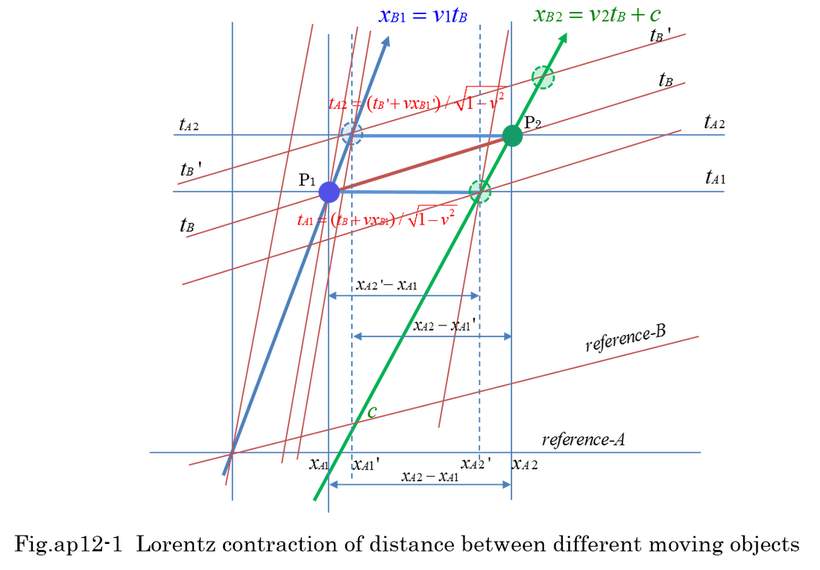
Supposing that P1 and P2 are moving uniformally in reference-B as shown in equation (ap12-1). The reference-B is moving with velocity(v) in reference-A. The velocity of P1 is v1, and the velocity of P2 is v2 in reference-B. Lorentz transformation is equation (ap12-2,3). Two points(P1, P2) are existing in reference-B at the same time(tB). However, these points are not existing at the same time in reference-A as shown in Fig.ap12-1. The simultaneity is important when considering the distance between two points.
The distance is expressed in equation (ap12-7) when tA=tA2. The distance is expressed in equation (ap12-8) when tA=tA1.
(xA2-xA1')/(xB2-xB1) and (xA2'-xA1)/(xB2-xB1) are different as shown in equation (ap12-7) and equation (ap12-8). When v1=0 and v2=0, the ratio of distance is equal to sqrt(1-v^2). It is exactly Lorentz contraction.
The distance is expressed in equation (ap12-7) when tA=tA2. The distance is expressed in equation (ap12-8) when tA=tA1.
(xA2-xA1')/(xB2-xB1) and (xA2'-xA1)/(xB2-xB1) are different as shown in equation (ap12-7) and equation (ap12-8). When v1=0 and v2=0, the ratio of distance is equal to sqrt(1-v^2). It is exactly Lorentz contraction.
<Appendix 13 --- Increase of inertia caused by the excitation of inner kinetic energy>
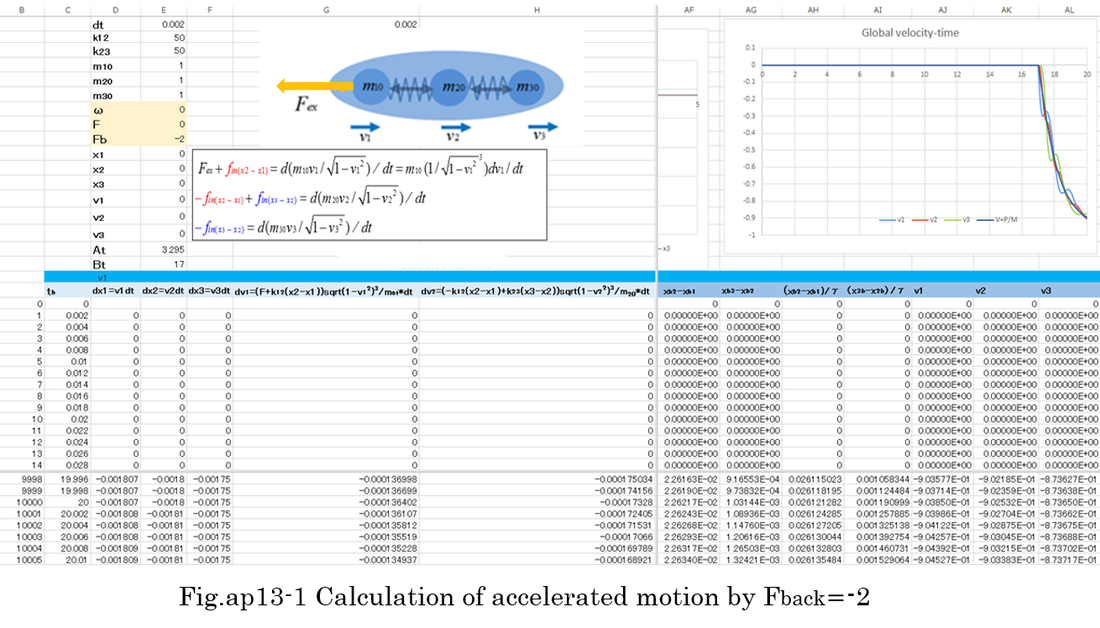
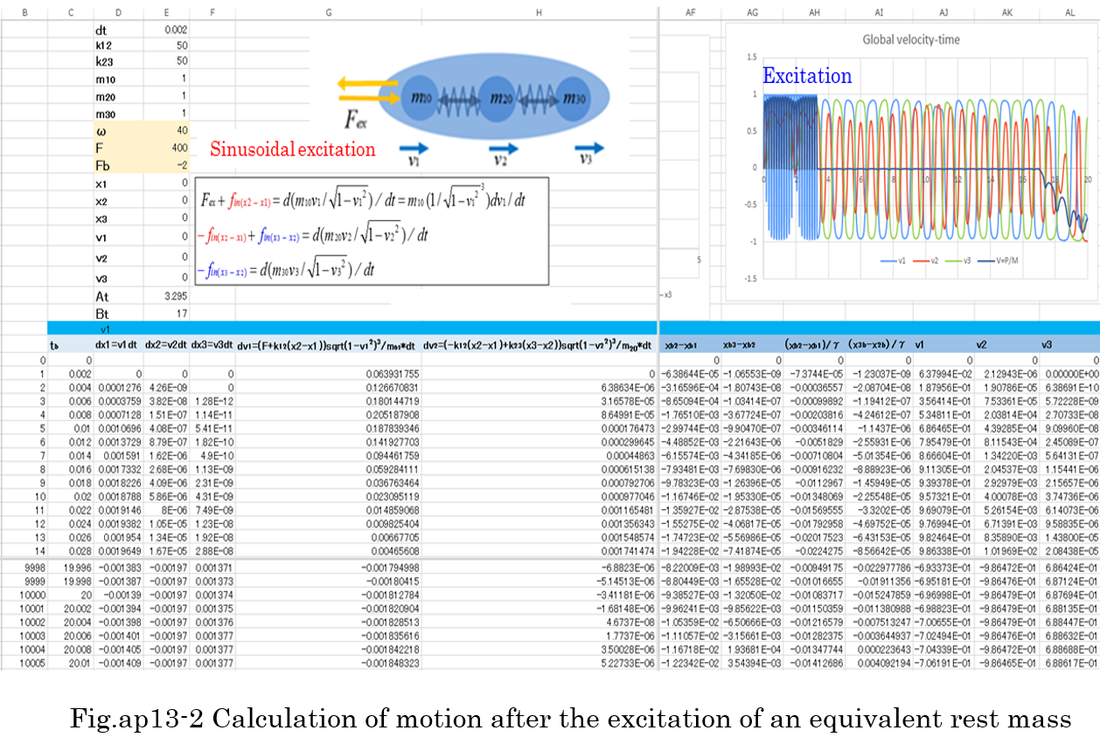
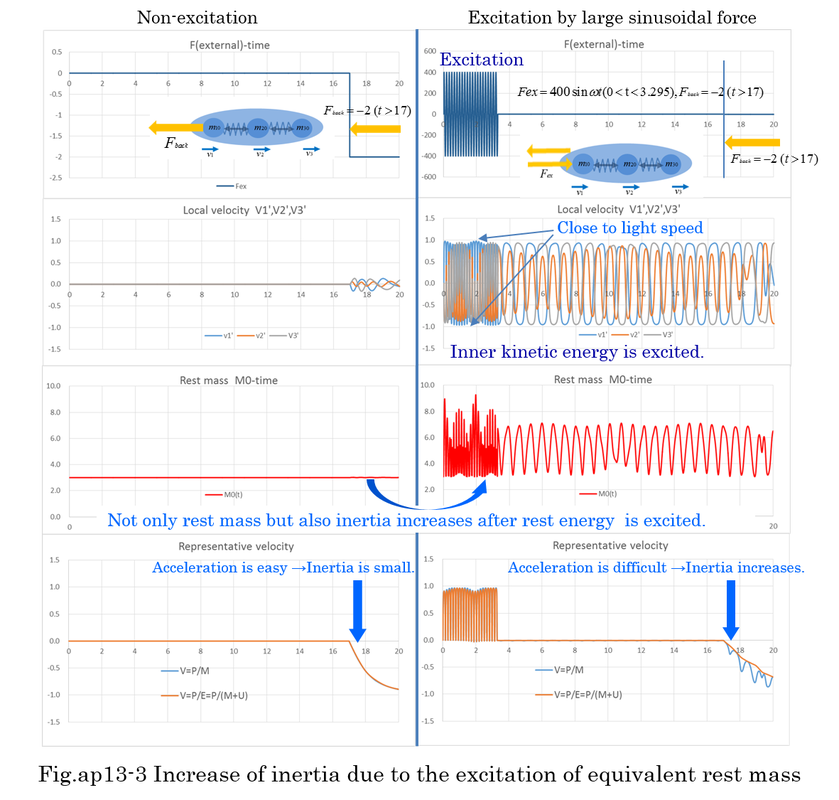
It is well known that the inertia of relativistic mass( M=M0/sqrt(1-V^2) ) becomes larger as an object moves faster. However, if many of inner particles or inner components which constitute an object oscillate faster within the body, does the inertia of an object really become larger? Even if representative velocity(V) is nearly zero, mathematical calculation proves that the inertia of an object increases when inner rest masses are previously excited by external force.
Let's suppose that an equivalent rest mass consists of three masses and two mass-less springs as shown in Fig.ap13-1,2. The first case is that the rest mass is not excited by sinusoidal force, and after 17 seconds, it is accelerated by the external force(Fback=-2, t>17). The second case is that the rest mass is severely excited by sinusoidal force for 3.295 seconds, and after 17 seconds, it is also accelerated by Fback . Inner kinetic energy increases by excitation. Local velocity v1',v2',v3' are oscillating with high speed, though representative velocity(V) is nearly zero. This means increase of rest energy. The bottom figure of Fig.ap13-3 indicates that the inertia of excited rest mass(M0) is larger than that of non-excited rest mass even if initial velocity(V) is nearly zero. Of course, relativistic mass(M) also increases gradually as the representative velocity(V) increases by adding the force(Fback).
Let's suppose that an equivalent rest mass consists of three masses and two mass-less springs as shown in Fig.ap13-1,2. The first case is that the rest mass is not excited by sinusoidal force, and after 17 seconds, it is accelerated by the external force(Fback=-2, t>17). The second case is that the rest mass is severely excited by sinusoidal force for 3.295 seconds, and after 17 seconds, it is also accelerated by Fback . Inner kinetic energy increases by excitation. Local velocity v1',v2',v3' are oscillating with high speed, though representative velocity(V) is nearly zero. This means increase of rest energy. The bottom figure of Fig.ap13-3 indicates that the inertia of excited rest mass(M0) is larger than that of non-excited rest mass even if initial velocity(V) is nearly zero. Of course, relativistic mass(M) also increases gradually as the representative velocity(V) increases by adding the force(Fback).
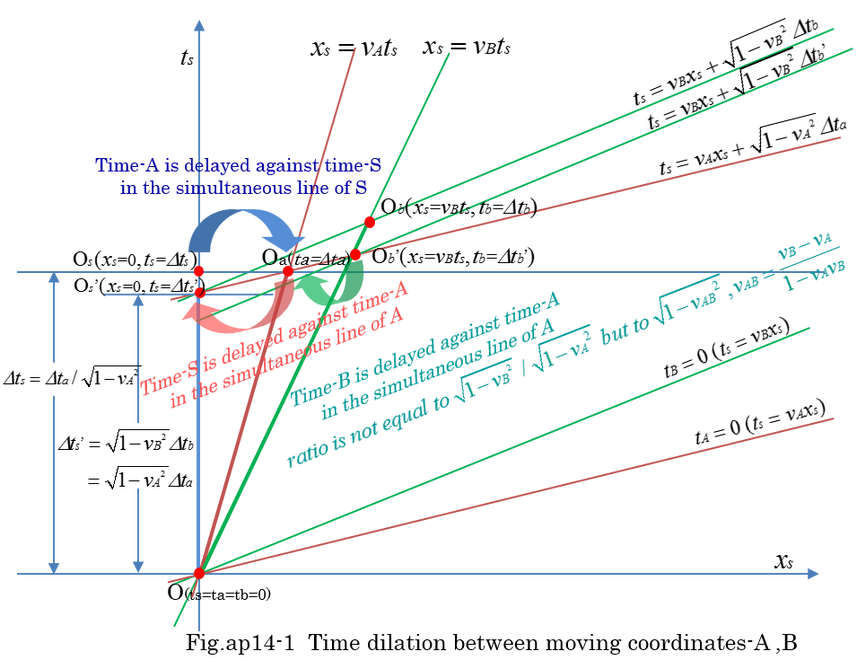
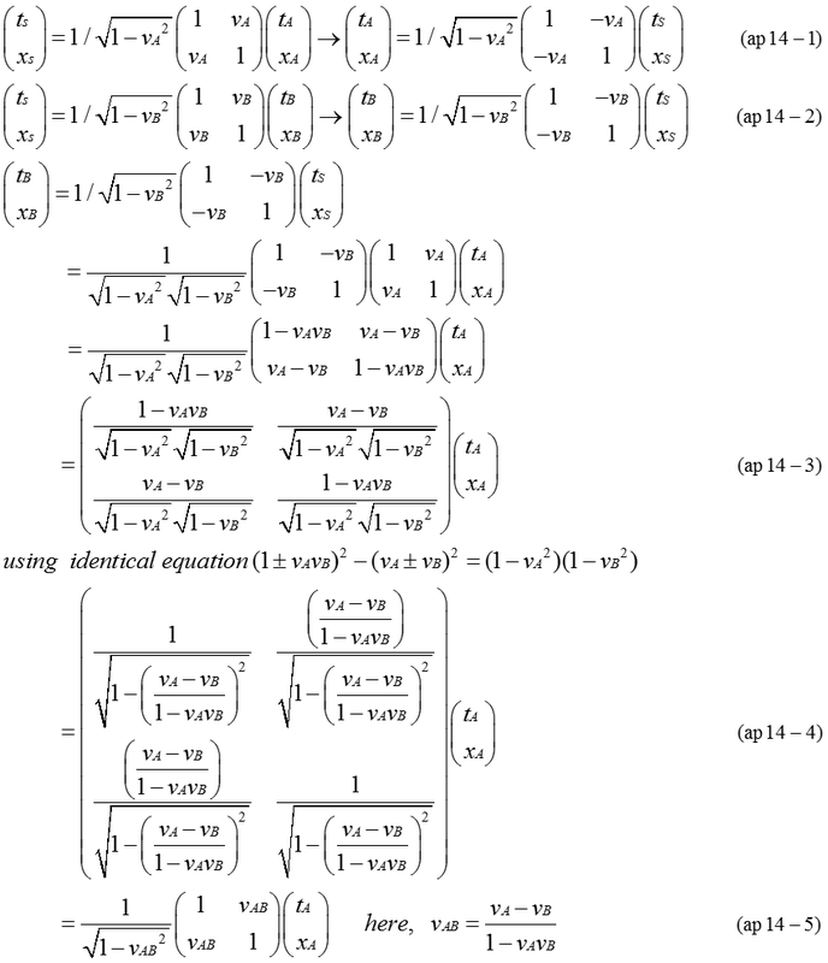
<Appendix 14 --- Time dilation between moving coordinates A and moving coordinates B>
Coordinates A and coordinates B are moving with the velocity va,vb respectively in stationary coordinates S. (xa,ta) is space-time in coordinates A, (xb,tb) is space-time in coordinates B, and (xs,ts) is space-time in stationary coordinates. ta is delayed by the ratio(ta/ts) of sqrt(1-vA^2). tb is also delayed by the ratio(tb/ts) of sqrt(1-vB^2). Concerning the time delay ratio between coordinates A and B, it is mistakenly expected that the time ratio of tb/ta is probably sqrt(1-vB^2)/sqrt(1-vA^2). If this supposition is right, the ratio is larger than 1 when va>vb. Therefore, this supposition is wrong. Fig.ap14-1 indicates space-time map. The correct ratio of tb/ta is sqrt(1-vAB^2) . Relative velocity between coordinates A and B is vAB=(vB-vA)/(1-vAvB). Equation (ap14-1,2,3,4,5) is calculation process using Lorentz transformation(S→B) and inverse Lorentz transformation(S→A). It must be considered that the delay occurs between Oa and Ob' in Fig.ap14-1. Using indirect relationship between Ob-Os' and Oa-Os' leads to a wrong time dilation between coordinates A and B. Time must be compared on the simultaneous line. Line Os'-Oa-Ob' is a simultaneous line in the coordinates A.
Furthermore, there are two ratio sqrt(1-vA^2) and 1/sqrt(1-vA^2) when we consider time dilation between stationary coordinates and moving coordinates A. Th relationship between blue arrow and red arrow in Fig.ap14-1 gives a proper reason why a stationary watch(or clock) and a moving watch are delayed each other.
Furthermore, there are two ratio sqrt(1-vA^2) and 1/sqrt(1-vA^2) when we consider time dilation between stationary coordinates and moving coordinates A. Th relationship between blue arrow and red arrow in Fig.ap14-1 gives a proper reason why a stationary watch(or clock) and a moving watch are delayed each other.
<Appendix 15 --- Concept of mass defect in special relativity >
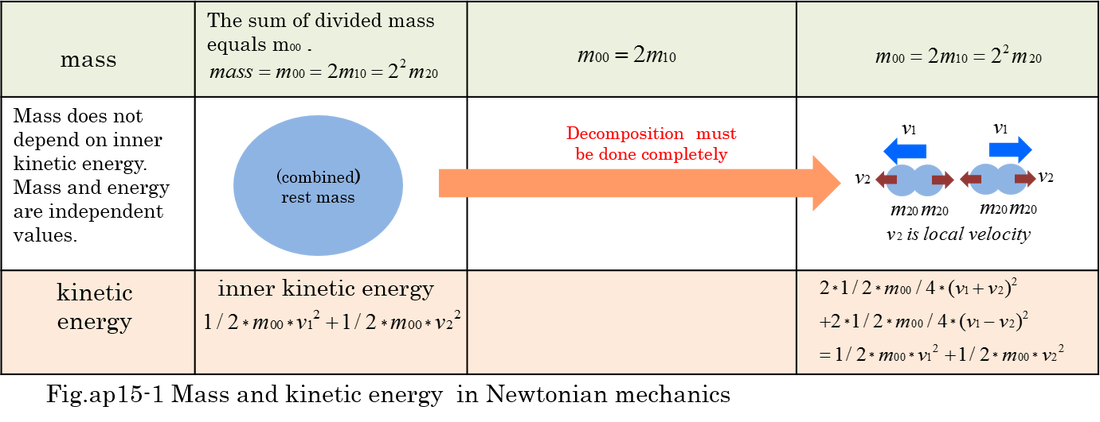
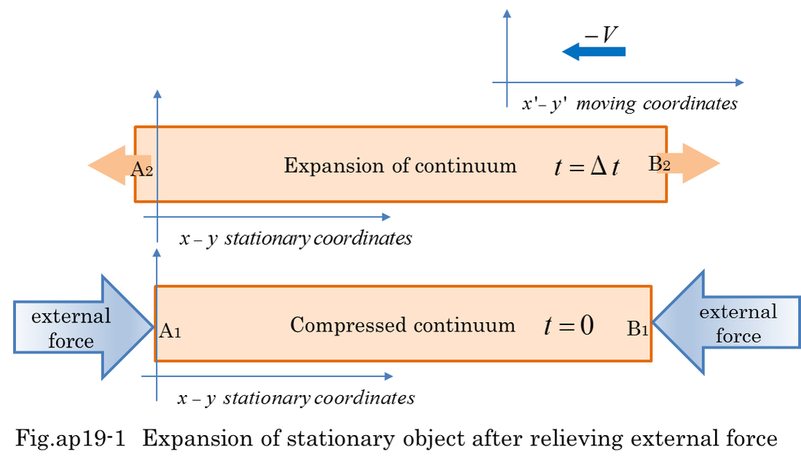
Before we discuss mass defect, it is necessary to review the mass in Newtonian mechanics. Both energy and mass conservation were basic foundation in physics. Mass was thought to be like a material which can be accompanied by kinetic energy. But, mass was quite different from energy in Newtonian mechanics. Mass is often divided by chemical reaction. The total of these divided masses never changes even if there is large heat generation in the process of chemical reaction. Fig.ap15-1 indicates that mass is independent of kinetic energy in Newtonian mechanics.
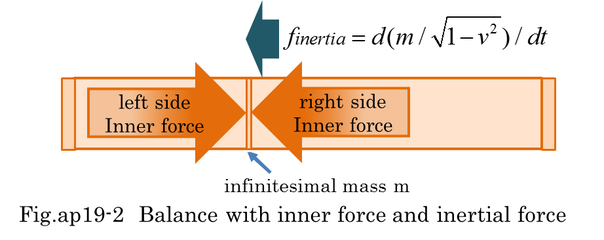
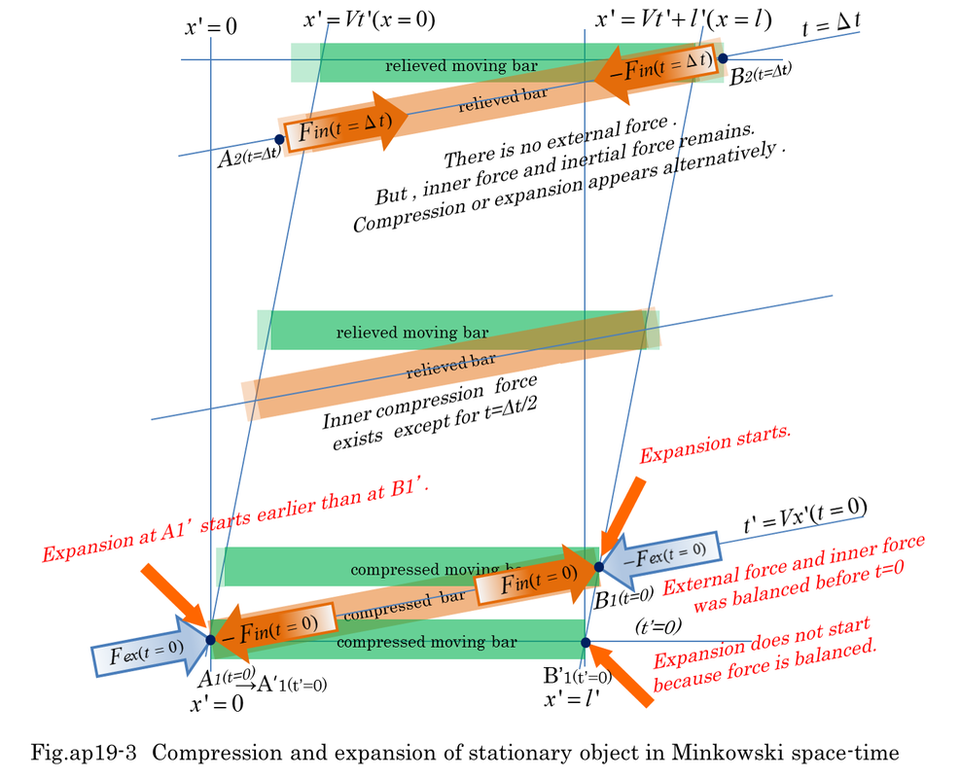
Rest mass(m00) is a stationary mass and it seems to have no visible kinetic energy. However, it was found that rest mass depends on inner kinetic energy after establishment of special relativity. When a lot of moving masses are combined to a stationary object, we can consider it to be a rest mass including kinetic energy. Fig.ap15-2 indicates that rest mass can be decomposed into small masses with kinetic energy. This means inner kinetic energy is a part of rest mass. Mass defect is exactly the same phenomenon that a lot of decomposed masses appear with visible kinetic energy. Therefore, the total of decomposed rest masses is less than m00 because of released kinetic energy. Energy conservation is strictly kept through the decomposition of rest mass. However, conservation of rest mass is not kept (m00>2m10>4m20) when the decomposition of rest mass is accompanied by the release of large kinetic energy.
<Appendix 16 --- Relativistic Tsiolkovsky rocket equation in case of constant momentum >
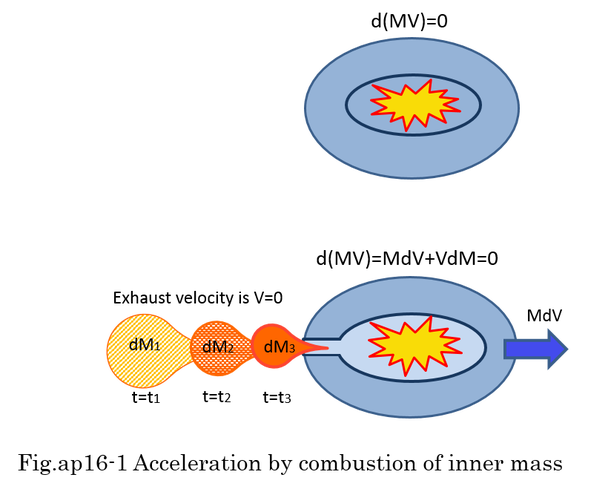
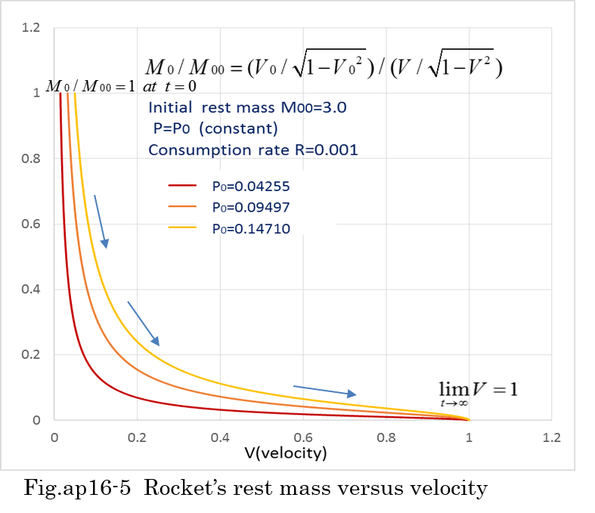
It is possible to accelerate mass without external force. By the continuous combustion of mass and exhaust of inner mass, mass can be accelerated. Fig.ap16-1 shows the combustion of mass. In the first case, mass is not accelerated because momentum is balanced and there is no separation of mass. In the second case, combustion gas is exhausted through the pipe. The mass of rocket decreases and the velocity of rocket increases. Relative velocity of separated mass(dM) is U against the rocket while the rocket is moving with the velocity(V). The rocket is accelerated to V+dV by the reaction force of dM. Therefore, the separation of mass occurred continuously. When relative velocity(U) of dM is equal to -V, dM is left with zero velocity in the global coordinates. Before the separation of dM, dM had the momentum of VdM and VdM→0 after the separation. -VdM contributes to the increase of MdV. Total momentum of the whole system is kept constant. This means that the momentum of right side mass is always equal to initial momentum K=P0(t=0). Because the velocity of dM is zero in the global coordinates, there is no change in momentum, that is dP=MdV+VdM=0. The integration of -VdM is equal to the integration of MdV. In this case, dM indicates the separation of mass. Rest mass(M0) also decreases according to the separation of mass(dM). Equation (ap16-1,2,3) are satisfied.
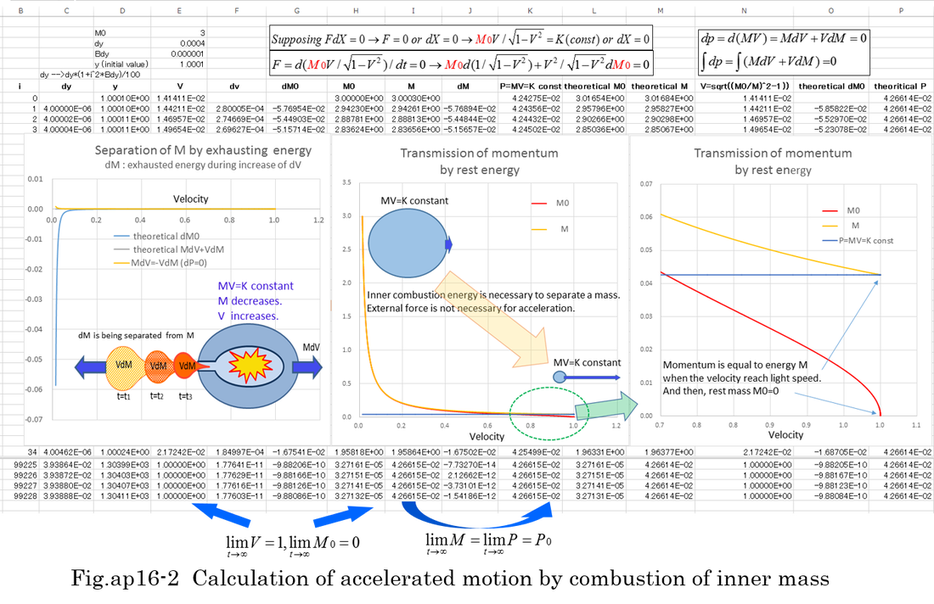
Needless to say, P=M0V/sqrt(1-v^2)=K satisfied equation (ap16-2). Fig.ap16-2 is an example of calculation. The result of numerical calculation of differential equation (ap16-2) is almost the same as MV=K(constant). y is defined as a function of 1/sqrt(1-V^2). As far as y is larger than1, y prevents V from exceeding light velocity 1 because V is V=sqrt(1-1/y^2).
If the combustion continues forever, rest mass(M0) approaches zero and the velocity(V) approaches 1. However, the momentum(P) is not zero, but it is still kept P0. That means P(t=∞)=MV=M(t=∞)=P0. In this respect, the result of numerical calculation and the simple equation MV=P0 is the same as P(t=∞)=M(t=∞)=P0.
If the combustion continues forever, rest mass(M0) approaches zero and the velocity(V) approaches 1. However, the momentum(P) is not zero, but it is still kept P0. That means P(t=∞)=MV=M(t=∞)=P0. In this respect, the result of numerical calculation and the simple equation MV=P0 is the same as P(t=∞)=M(t=∞)=P0.
The above calculation does not say anything about time. When the rate of combustion is decided as dM0=-R*dτ(τ is proper time), the relationship between t and V can be decided. As it is well known, the increment of proper time is dτ=sqrt(1-V^2)dt. When the initial rest mass(M00) is consumed completely at the time of τ=M00/R in the rocket, time(t) on the earth is infinite because V approaches 1.
Equation (ap16-4) means that rest mass(M0) is consumed at the rate of R. From equations (ap16-1),(ap16-4), equation (ap16-5) is obtained.
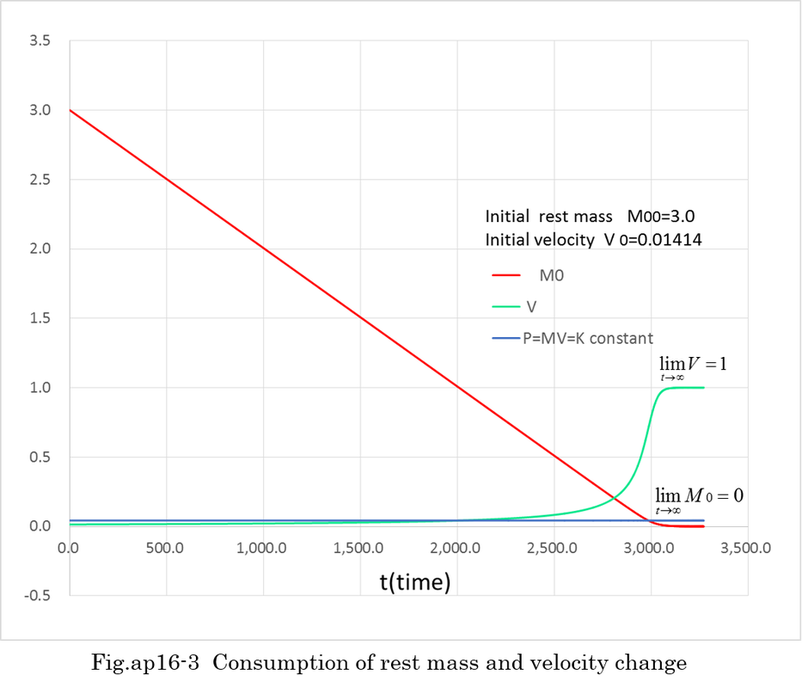
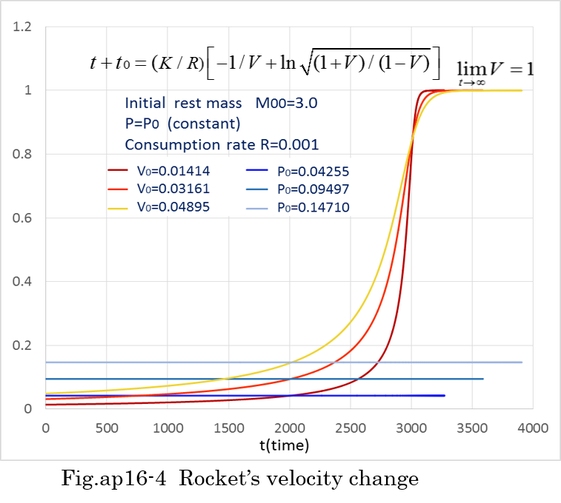
By differentiating equation (ap16-5), equation (ap16-6) is obtained. Equation (ap16-7),(ap16-8) are procedures of calculation. Final result is equation (ap16-9). Fig.ap16-3 indicates how the initial mass is consumed and the velocity of rocket is accelerated.
Equation (ap16-4) means that rest mass(M0) is consumed at the rate of R. From equations (ap16-1),(ap16-4), equation (ap16-5) is obtained.
By differentiating equation (ap16-5), equation (ap16-6) is obtained. Equation (ap16-7),(ap16-8) are procedures of calculation. Final result is equation (ap16-9). Fig.ap16-3 indicates how the initial mass is consumed and the velocity of rocket is accelerated.
Equations (ap16-10,11,12,13) are obtained from equations (ap16-5),(ap16-9). Equation (ap16-9) indicates that the transition of velocity(V) depends on the ratio of (P0/R). It also indicates there is no difference in the shape of the function except for time scale and time shift. If the consumption rate is large, the acceleration of mass is large. Fig.ap16-4 indicates results of calculation. The moving rocket with small momentum is not easy to be accelerated in the early stage, but it is rapidly accelerated up to the light velocity in the final stage.
Fig.ap16-5 indicates the relationship between consumption of rest mass(M0) and velocity(V). The velocity of rocket finally reaches 1 (light speed). As it is explained, rest mass(M0) is consumed completely when proper time(τ) is M00/R. Although τ is finite, time(t) is infinite because of time dilation.
<Appendix 17 --- Calculation of motion of a mass including inner potential energy>
A group of masses consists of a lot of relativistic masses and it forms an equivalent rest mass. As it is explained in page-3, this is completely consistent with the formula of velocity composition in case of free particles. Further more, it is necessary to study the method on how we can treat the energy of a group of masses restrained by inner potential force. We must distinguish external potential energy and inner potential energy. The force in the external potential field belongs to external forces. In general, physical object can be decomposed into inner elements like mass and spring. The numerical calculation of motion is done for the model that two masses are connected by a spring. That means the object has inner potential energy(Uin). Here, the external potential energy is beyond consideration because it has interaction with outside of mass(M). If we discuss the external potential energy, total system must be considered including outer masses. It is almost meaningless whether the external potential energy contributes to inertia of a mass. Fig.ap17-1 indicates an example of calculation. This Excel's program is made to calculate the motion of three masses. By making second mass(m20) very small value(0.000001), the calculation model can be applied for two-mass motion.
As shown in Fig.ap17-2, the objects is accelerated by external force(Fex=1), two masses gradually have kinetic energy and inner potential energy. Total energy becomes constant after acceleration for 3 seconds and the the object is decelerated by external force(Fex=-1) until the object velocity becomes zero. Then, visible kinetic energy is zero, but the sum of inner potential energy and inner kinetic energy reach a certain constant value which is larger than that of start time(t=0). The sum of inner potential energy and kinetic energy is zero at t=0. Increase of energy is equal to ∫Fexdx=Δ(M+Uin) from t=11 to 20. If mass(M) has not inner structures, there is only increase or decrease of visible kinetic energy. Increase of energy can be saved within the mass(M) in the process of acceleration and deceleration. We must give a reasonable concept that increase of inner potential energy can be considered as increase of inertia(mass).
Fig.ap17-3 indicates the relationship between energy and velocity. However, including inner potential energy, it seems difficult to understand that the total energy E(=M+Uin) can be expressed by E=E0/sqrt(1-V'^2) because virtual velocity(V') is not equal to V,v1,v2,v3. But, after acceleration or deceleration is finished, total energy and momentum turns to constant value. And so, there seems to be something like a constant velocity(V'). Using the virtual velocity, rest energy(E0) can be defined even though M0 does not contain inner potential energy. When the total momentum is zero(P=0), V=V'=0 and E=E0. What does E0 means in the period( t=0 ~11)? What kind of velocity is true? Relativistic mass M is always expressed by M0/sqrt(1-V^2) supposing that M0 is not constant but invariant in any inertial frame. External force(Fex) increases not only visible kinetic energy but also inner kinetic energy and inner potential energy when physical object has inner structure.
dE/dP=V is obtained from two equations(dE=FdX,Fdt=dP). There is an interesting method that can calculate dE/dP=v1 even if dP=0 theoretically. Of course, v1 is strictly calculated from differential equation. When external force is modified from Fex by adding very small random force, We can calculate dE/dp avoiding dp=0 and calculate the motion of masses as if Fex=0 and dP=0. To give the evidence, Fig.ap17-4 indicates the effect of large random force. Although the average of random force is to be zero, the representative velocity V(t=11 ~ 20) happened to be not zero.
Back to the main topic on inner potential energy, some analysis about E=E0/sqrt(1-V'^2) is now examined. Momentum P=MV is well known, but P=EV' is not. Equation (ap17-1) means that momentum is originally a flow of energy. Equation (ap17-2) is an extended force. From these new definitions, E=E0/sqrt(1-V'^2) is introduced. In Fig.ap17-3, E=E0 (t=11~20) is constant value including inner potential energy and inner kinetic energy and rest mass(m10,m20).
Following analysis shows that total energy of a group of mass can be treated as E=E0/sqrt(1-V'^2). Energy(E) includes visible kinetic energy, inner potential energy, inner kinetic energy and inner rest masses. M0' is not equal to M0, but when V'=V=0, M0'=M0. It is difficult to accept this result of analysis because Uin is intentionally separated to U0/sqrt(1-V'^2) and U0*V'^2/sqrt(1-V'^2) in equation (ap17-7). Most uncertain equation might be P=MV=EV'. However, Fig.ap17-3 indicates M0'=E0-U0 is completely equal to Σmi0/sqrt(1-vi'')^2 and E is dependent on V'. In Excel's numerical calculation, it is proved that U0*V' is completely equal to Σmi0Vi''/sqrt(1-vi''^2). It seems to be reasonable that E should be finally expressed by (M0'+U0)/sqrt(1-V'^2).
In case of spring's elastic energy, inner potential energy(Uin) is always positive value. Then, the absolute value of V'=MV/(M+Uin) is less than the absolute value of V. This condition means that V' never exceeds light velocity because V never exceeds light velocity.
In case of spring's elastic energy, inner potential energy(Uin) is always positive value. Then, the absolute value of V'=MV/(M+Uin) is less than the absolute value of V. This condition means that V' never exceeds light velocity because V never exceeds light velocity.
Fig.ap17-5 is Excel's numerical calculation of the position of mass and spring's displacement. Inner rest m20 is almost zero(0.000001), then, x2 is the average of spring displacement. X is the center of momentum because V is expressed by V=P/M=(m1v1+m2v2)/(m1+m2). V' is newly defined as P/E. The result of integration of V' indicates that the position of X' is between X and X2. X' seems to be the center of total energy which includes inner potential energy, inner kinetic energy, inner rest mass and visible kinetic energy. As shown in the second case of Fig.ap17-5, when spring is rigid and external force(Fex) is small, X, X2 and X' become convergent to the same value even if x1 and x3 oscillate alternately.
Does the total energy including inner potential has inertia? In the summary of top page , (15) indicates that inner kinetic energy contributes inertia. However, it never be a reasonable reason that E=Mc^2 is almighty equation about all kinds of energy. As for inner potential energy, equations (ap17-7,8,9,10) indicate that inner potential can be considered as a part of inertia. As for equation (ap17-7) , it might be unnatural condition. Nevertheless, numerical calculation proves this concept seems to be reasonable. In Fig.ap17-6, dV'/dt is compared with dV/dt.
After deceleration, velocity of mass becomes zero(V=V'=0). Although x1 and x3 oscillate alternately, the center of mass(M) does not move . The summation of inner potential and inner kinetic energy is constant, then, potential energy is maximum when kinetic energy is minimum. At this point of time, how is the inertia of a group of masses ? By loading external force(Fex=-1) when mass(M) is at rest, the motion of M can be calculated numerically to examined whether the inertia is kept constant. Numerical calculation shows that dV'/dt is constant as long as E0 is the same value and V'=V=0. Even if inner kinetic energy is minimum, dV'/dt is kept constant because inner potential energy is maximum. On the other hand, dV/dt is proportional to 1/M0. E0 is equivalent to rest energy including inner potential energy and inner kinetic energy. E0 is also invariant in any reference coordinates but not constant concerning time change.
After deceleration, velocity of mass becomes zero(V=V'=0). Although x1 and x3 oscillate alternately, the center of mass(M) does not move . The summation of inner potential and inner kinetic energy is constant, then, potential energy is maximum when kinetic energy is minimum. At this point of time, how is the inertia of a group of masses ? By loading external force(Fex=-1) when mass(M) is at rest, the motion of M can be calculated numerically to examined whether the inertia is kept constant. Numerical calculation shows that dV'/dt is constant as long as E0 is the same value and V'=V=0. Even if inner kinetic energy is minimum, dV'/dt is kept constant because inner potential energy is maximum. On the other hand, dV/dt is proportional to 1/M0. E0 is equivalent to rest energy including inner potential energy and inner kinetic energy. E0 is also invariant in any reference coordinates but not constant concerning time change.
If you need to check the calculation of motion of mass and spring system, click the following file.
| mass_and_inner_potential_20150415.xlsx | |
| File Size: | 26338 kb |
| File Type: | xlsx |
< Appendix 18 --- Transverse velocity of light in moving coordinates>
It is well known light velocity is constant in any reference frame as long as the direction of light velocity coincides with the direction of moving x-axis. Lorentz transformation is done as to x and t. y is the same as y'. Is light beam velocity equal to 1 when coordinates moves vertically against light beam? Nobody doubts the light beam velocity is equal in any direction in stationary coordinates. However, it must be confirmed that transverse light velocity is the same as c=1 when the light beam is observed in moving coordinates B. Fig.ap18-1 indicates the calculation of the position of light which is emitted along the stationary y-axis. The direction of light beam changes according to the velocity of moving coordinates B. Nevertheless, the velocity is surely equal to1 in coordinates B. Even if the light is emitted in all directions, the light speed in any direction is equal to1. In Fig.ap18-1, light beam A1,A2 are transformed to B1,B2 respectively. Light beam A2 is the one which is emitted from the origin of coordinates A to the point(x=vt,y=sqrt(1-v^2)*t).
Fig-ap18-2 indicates the spherical light waves in moving coordinates. There is always one light beam which moves along y' axis in case of spherical waves as it is explained in Fig.ap18-1. Refer to Fig.ap4-1,2 in appendix 4.
In addition, if the light beam is continuously emitted along y-axis in stationary coordinate A, the top of beam is observed as diagonal line in coordinates B, but actually , it looks like the light beam is being emitted from moving light source to L2 because light emission continues one after another. It is often misunderstood that the same top of light goes vertically from L1 to L2 in the moving coordinates B. The light beam consists of many different lights which were emitted at different times.
This means that the top of light beam goes diagonally when you move the source of light beam. It is a similar case of throwing a ball from the moving train's window. If the moving light beam would go vertically against moving x'-axis, absolute stationary space could be decided. The velocity of sound propagation does not depend on the motion of object in the fluid which corresponds to absolute space. Special relativity claims that there is not such a case in case of light propagation. The direction of light beam of moving light source always goes vertically in the same moving coordinates and the direction of stationary transverse light beam depends on the velocity of moving coordinates B.
In addition, if the light beam is continuously emitted along y-axis in stationary coordinate A, the top of beam is observed as diagonal line in coordinates B, but actually , it looks like the light beam is being emitted from moving light source to L2 because light emission continues one after another. It is often misunderstood that the same top of light goes vertically from L1 to L2 in the moving coordinates B. The light beam consists of many different lights which were emitted at different times.
This means that the top of light beam goes diagonally when you move the source of light beam. It is a similar case of throwing a ball from the moving train's window. If the moving light beam would go vertically against moving x'-axis, absolute stationary space could be decided. The velocity of sound propagation does not depend on the motion of object in the fluid which corresponds to absolute space. Special relativity claims that there is not such a case in case of light propagation. The direction of light beam of moving light source always goes vertically in the same moving coordinates and the direction of stationary transverse light beam depends on the velocity of moving coordinates B.
Fig.ap18-3 indicates that the light cone spreads in Minkowski space -time. Light cone includes both coordinates A and coordinates B. The velocity is the same both in coordinates A and moving coordinates B. We must remember that the length(P1P3) does not a real length in Minkowski space-time. According to the formula, Δs=sqrt(Δx^2-Δt^2)=sqrt(Δx'^2-Δt'^2) is a 4-dimensional length. In the simultaneous world (Δt'=0), Δs is a real distance. Plane equation (ap18-1) is a simultaneous world in coordinates B. Light cone is expressed by equation (ap18-2). The line of intersection is an ellipse, but it also a circle(x'^2+y'^2=1) in the simultaneous world(t'=constant). Minor axis is equation (ap18-3). From the calculation of intersection, the diameter which is equivalent to major axis is equation (ap18-4). It is confirmed equation (ap18-3) is equal to equation (ap18-4). This means light velocity is the same in both direction of x'-axis and y'-axis in coordinates B.
< Appendix 19 --- Compression and expansion of elastic continuum in Minkowski space-time>
Fig-ap19-1 indicates a compressed elastic body by the external forces. When t=0, the object is relieved from external forces at both sides(A1 and B1) and starts to vibrate. At t=Δt, the length of object reaches maximum length. The center of object does not move in stationary coordinates(x-t space-time). This motion also can be observed in moving coordinate(x'-t' space-time). The velocity of moving coordinates is -V in stationary coordinates(x-t space-time). Therefore, the object moves to right side even if there is no external force. As it is well known, when you are in moving coordinates, the time of both ends of the object are different in Minkowski space-time. The right side force still remains for a while because the time of right side edge delays a little bit of time.
Someone might think the object must be decelerated to the left side because left side external force is zero while right side external force remains. It looks like there is something paradoxical. However, it is not a paradox at all.
Someone might think the object must be decelerated to the left side because left side external force is zero while right side external force remains. It looks like there is something paradoxical. However, it is not a paradox at all.
We need to know the balance of force. The object consists of a lot of infinitesimal masses(m). Fig.ap19-2 indicates that infinitesimal mass(m) receives two forces from both sides and generates inertial force by it's accelerated motion. Even if there is no external forces, there exists inner forces in the elastic object. It is similar to an example that a compressed spring is being relieved from compression. Both ends of expansion are illustrated in a different color. Fig.ap19-3 indicates that the vibration of the object in Minkowski space-time. Before t=0, external forces and inner forces are balanced and the object is fixed. The length of the object becomes natural length when t=Δt/2. The length of the object becomes maximum length when t=Δt because inertial force continues expansion against elastic force.
Fig.ap19-4 indicates that the vibration displacements of moving object from uniform motion(x'=Vt', X'=Vt'+l') in the moving coordinates. Both edges(A1' and B1') of moving object is in the same time(t'=0) in the moving coordinates(x'-t' space-time), but two points are in a different time each other in the stationary coordinates(x-t space time). A1' starts expansion and B1' does not start expansion at first, therefore, it looks like the objects is decelerated. However, the average position of object moves according to the uniform motion(x'=Vt', X'=Vt'+l'). In Fig.ap19-4, each initial displacement at both ends of the object is supposed to be zero when both sides are compressed at t'=0.
< Appendix 20 --- Different time dilation ratio due to the confusion about Minkowski x-y-t space >
In case of Minkowski 2 dimensional x-t space, time dilation is well known. Time dilation ratio is sqrt(1-v^2) or 1/sqrt(1-v^2). We must remember that each different x position in stationary coordinates has different time of moving coordinates. However, some people say that time dilation ratio varies according to the direction of light beam in the x-y-t coordinates. Fig.ap20-1 shows the process to the wrong conclusion. Two light beams are emitted from the originO0 to P2 and P3 at t=0. One light beam goes along y axis and reaches P2 at t=1. The other is diagonally directed to P3 and reaches P3 at t=1. These light path are also observed in moving coordinates which moves with the velocity -v. The length of O0P2, O0P3 are equal to the time(t=1) because light velocity c is equal to (c=1). The length of O1P2, O1P3 is equal to the time t1'and t2' respectively because light velocity c is always equal to (c=1). However, the length O1P3 is longer than O1P2 in moving coordinates. Then, time dilation depends on the direction of light. Although the conclusion is completely wrong, this thinking process looks like a right conclusion. Where is a misunderstanding or confusion about space-time?
The thinking process shown in Fig.ap20-1 is based on nothing other than Galilean transformation. Is the length of O1P2, O1P3 truly the correct length in moving coordinates? Do you think that two lines of O1P2, O1P3 exist in simultaneous world(t=1) in moving coordinates?
Fig.ap20-2 indicates that the optical path O2P2 exists in the time(t'=1/sqrt(1-v^2)) and the optical path O3P3 exists in different time. These two paths are contained in different diagonal planes. On the other hand, in Fig.ap20-1, it was mistakenly supposed that false optical path O1P2, O1P3 exist in the time(t=1) . Considering space-time, light path O0P2 and O0P3 are contained in the yellow light cone surface. It is difficult to image actual optical path O0P2,O0P3. Then, we substitute virtual optical path(O2P2,O3P3) for O0P2,O0P3. Each path O2P2,O3P3 exists in different time in moving coordinates.
Fig.ap20-2 indicates that the optical path O2P2 exists in the time(t'=1/sqrt(1-v^2)) and the optical path O3P3 exists in different time. These two paths are contained in different diagonal planes. On the other hand, in Fig.ap20-1, it was mistakenly supposed that false optical path O1P2, O1P3 exist in the time(t=1) . Considering space-time, light path O0P2 and O0P3 are contained in the yellow light cone surface. It is difficult to image actual optical path O0P2,O0P3. Then, we substitute virtual optical path(O2P2,O3P3) for O0P2,O0P3. Each path O2P2,O3P3 exists in different time in moving coordinates.
Diagonal simultaneous line equations (ap20-1,4,5) are obtained from Lorentz transformation. Diagonal optical path O3P3 exists in the the pink colored simultaneous plane (t'=(v*XP4+1)/sqrt(1-v^2)). Equation (ap20-5) indicates that the position of XP4 at t=1means the time shift of Δts=V*XP4/sqrt(1-v^2) in moving coordinates. Optical path length O2P2 is equal to 1/sqrt(1-v^2) that is exactly the time 1/sqrt(1-v^2) because light velocity is always c=1 in any reference coordinates.
Do not confuse the calculation result of optical path length O3P3. Originally, the position XP4 has time shift Δts in moving coordinates shown by equation (ap20-5). Then, time dilation ratio between stationary coordinates and moving coordinates is common whether light path is diagonal or not.
< Appendix 21 --- Equivalent rest mass composed of twin masses with vertical inner motion to x-axis >
In general, rest mass is composed of a lot of relativistic masses. In page-3, it is mathematically proved that equivalent rest mass of twin masses with inner motion along x-axis is summation of inner relativistic masses.
Fig.ap21-1 shows two kinds of moving mass with velocity v1. Inner motion in case A is parallel to x-axis. On the other hand, inner motion in case B is perpendicular to x-axis. It must be proved that equivalent rest mass is summation of relativistic masses as well as case A. We must refer to x-y-t Lorentz transformation matrix equation(ap11-2) again. Comparing Fig.ap21-1 with equation(ap11-2), we should be careful to notice that v1 must be exchanged for v2. In this section, vector v2 is converted by Lorentz transformation matrix.
Fig.ap21-1 shows two kinds of moving mass with velocity v1. Inner motion in case A is parallel to x-axis. On the other hand, inner motion in case B is perpendicular to x-axis. It must be proved that equivalent rest mass is summation of relativistic masses as well as case A. We must refer to x-y-t Lorentz transformation matrix equation(ap11-2) again. Comparing Fig.ap21-1 with equation(ap11-2), we should be careful to notice that v1 must be exchanged for v2. In this section, vector v2 is converted by Lorentz transformation matrix.
Exchanging v1 for v2, and considering x component of v2 and y component of v1 are zero, equation(ap11-2) becomes relatively simple.
Although each velocity(v3y) is not zero, Fig.ap21-2 indicates that total momentum of twin mass is p3x, and P3y=0. Calculation of mass and momentum using Lorentz matrix leads to the fact that equivalent rest mass is summation of relativistic masses. Equation(ap21-6,7) is similar to equation(2-23,24). This result is consistent with the concept that rest mass contains inner kinetic energy. When mass system moves with representative velocity V, total energy is expressed by E=m=m0/sqrt(1-V^2). E0=m0 (V=0) means that mass system which is considered as rest mass(m0) does not move in a certain reference frame. Do not forget that rest mass such as desk, chair, vehicle, mountain contains inner kinetic energy.
< Appendix 22 --- An example that rest mass is composed of many relativistic masses in x-y-t space >
Appendix 9 and Appendix 21 indicate examples that rest mass(M0) is composed of hexagon or twin of relativistic masses in two special cases. In both cases, the assembly of relativistic masses(mi) can be expressed by typical equation M=M0/sqrt(1-v^2).
Although an example is the case of x-y-t space, not x-y-z-t space, it must be generally shown that rest mass consists of many relativistic masses which have multiple directions of momentum. To make it easy to calculate Lorentz matrix, the rotated coordinates X'-Y' is considered. Furthermore, moving local coordinates x-y is considered. As Fig.ap22-1 is shown, the direction of representative velocity(v1) coincides with X'-axis and x-axis. The components of velocity vector(v1) are simply expressed by (v1,0) in coordinate X'-Y'. Equation (ap22-1) indicates that total momentum (Px,Py) of rest mass is zero in the moving local coordinates x-y. This means rest mass(M0) is at rest in the coordinate x-y, but, individual rest mass(mi0) is not at rest.
Although an example is the case of x-y-t space, not x-y-z-t space, it must be generally shown that rest mass consists of many relativistic masses which have multiple directions of momentum. To make it easy to calculate Lorentz matrix, the rotated coordinates X'-Y' is considered. Furthermore, moving local coordinates x-y is considered. As Fig.ap22-1 is shown, the direction of representative velocity(v1) coincides with X'-axis and x-axis. The components of velocity vector(v1) are simply expressed by (v1,0) in coordinate X'-Y'. Equation (ap22-1) indicates that total momentum (Px,Py) of rest mass is zero in the moving local coordinates x-y. This means rest mass(M0) is at rest in the coordinate x-y, but, individual rest mass(mi0) is not at rest.
The direction of X'-Y' axis and x-y axis can be chosen without losing the generality of discussion. Lorentz matrix becomes simple by matching X'-axis and x-axis with the direction of v1. Of course, all the components of individual local velocity(vi) change according to the rotation of coordinates x-y.
By summing equation (ap22-3) and using equation (ap22-1), equation (ap22-4,5,6,7) are obtained. Equation (ap22-7) indicates typical relativistic mass and relativistic momentum in the rotated stationary coordinates X'-Y'. The way of thinking that rest mass and kinetic energy are completely different things should be avoided. Rest mass is made of a lot of relativistic masses. Total momentum of rest mass is zero in a certain inertial coordinates even if individual constituent(mi0) is moving.
<Reference>
1 Gary Oas, On the abuse and use of relativistic mass, physics.ed-ph 21 Oct 2005 p1-2
2 L. B. Okun (1989),"The Concept of Mass" Physics Today 42 (6): p31–36,
tthp://www.itep.ru/theor/persons/lab180/okun/em_3.pdf
3 Max Jammer (1997), Concepts of Mass in Classical and Modern Physics, Courier Dover Publications,
p179, ISBN 0486299988
4 http://en.wikipedia.org/wiki/Mass_in_special_relativity
5 http://en.wikipedia.org/wiki/Lorentz_transformation
6 http://eman-physics.net/relativity/contents.html
7 http://en.wikipedia.org/wiki/Wave_equation
Notification
This article is published by Nobuo Miyaji. When you need to publish a portion of equations and figures in this article,
you should get approval from Nobuo Miyaji by e-mail. e-mail nobuo.miyaji@hotmail.co.jp
1 Gary Oas, On the abuse and use of relativistic mass, physics.ed-ph 21 Oct 2005 p1-2
2 L. B. Okun (1989),"The Concept of Mass" Physics Today 42 (6): p31–36,
tthp://www.itep.ru/theor/persons/lab180/okun/em_3.pdf
3 Max Jammer (1997), Concepts of Mass in Classical and Modern Physics, Courier Dover Publications,
p179, ISBN 0486299988
4 http://en.wikipedia.org/wiki/Mass_in_special_relativity
5 http://en.wikipedia.org/wiki/Lorentz_transformation
6 http://eman-physics.net/relativity/contents.html
7 http://en.wikipedia.org/wiki/Wave_equation
Notification
This article is published by Nobuo Miyaji. When you need to publish a portion of equations and figures in this article,
you should get approval from Nobuo Miyaji by e-mail. e-mail nobuo.miyaji@hotmail.co.jp